Split cotters

[Martin KyteParticipant @martinkyte99762]

Stating the obvious. George Thomas is largely aiming at a scribe,dot punch and drill audience Hemmingway are advocating a co-ordinate machined fixture produced on a vertical mill which is very likely to have a DRO in morst cases.

The curved pads ensure that the clamped bar is not marked. The critical dimension is actuallt the gap between the two pads when closed. Half the angle between the two contact points of the pads and the centre of the clamped bar will be the minimum effective taper which must be at least the minimum for a self releasing taper. If G is the gap and D is the diameter of the bar then the taper is arcsine (G/2)/D unless I've muddled my maths.

The clearence value of 20 or 30 thou does comeinto it.

regards Martin

[duncan webster 1Participant @duncanwebster1]

Yup, you've muddled the maths, it is arcsine (G/D). This site suggests that the magic number is 7 degrees PrcMac

and as sin(7) = 0.122 so you won't go far wrong with G = D/8, I'd make it a bit bigger just to be safe.

[Martin KyteParticipant @martinkyte99762]

Ah I was taking the 'gap' to be the distance between the two pads so I divided it by 2 to get the distance from the mid point to the start of the contact point or the oposite side of the triangle. But then I am not sure how tapers are generally defined so I went for half angle although I didn't say so.

I also mistyped the last bit, the point of which was that the clearance of 20 or 30 thou is irrelevent (I meant to type "does not come into it".)

G=D/8 sounds good to me with a taper target of greater than 7 degrees.

cheers Duncan

regards Martin

[Michael GilliganParticipant @michaelgilligan61133]

Martin & Duncan

It’s not worth worrying about … but I find that analysis difficult to grasp

Surely there are more variables involved in analysing the vectors

Where exactly are you assuming that either ‘locking’ or ‘self-releasing’ takes place ?

… is the diameter of the two ‘half-nuts’ [to use Duplex’s terminology] irrelevant ?

MichaelG.

[Martin KyteParticipant @martinkyte99762]

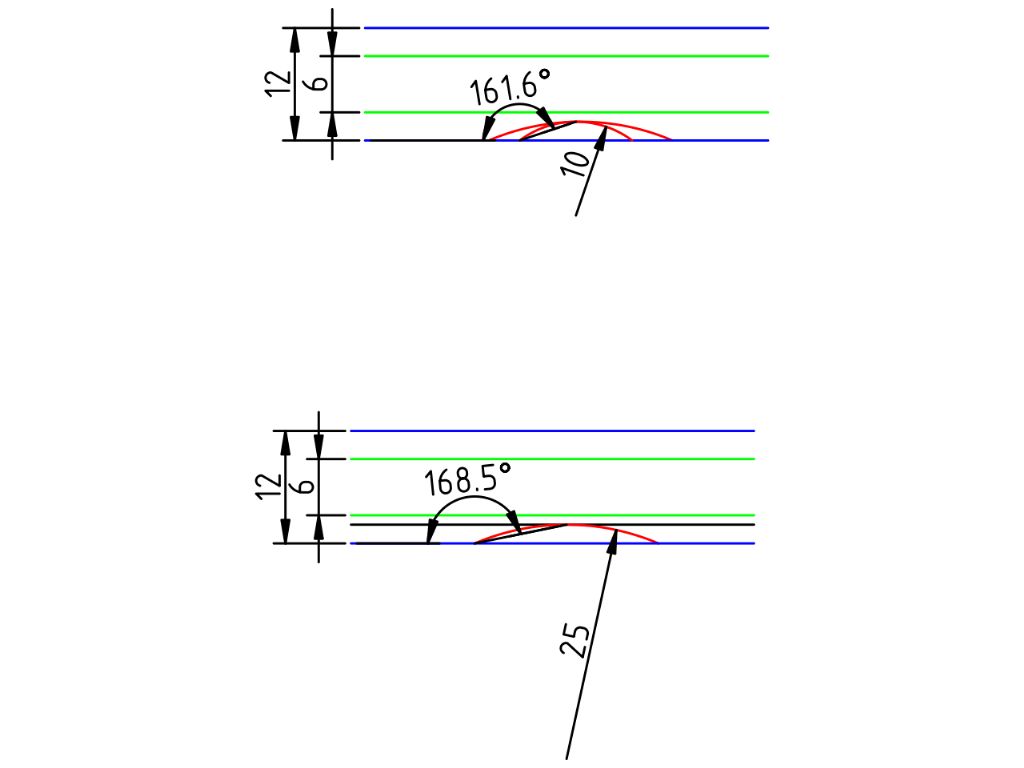
My thinking was that the curved section of the pad forms a taper that increses along it's length and is at it's minimum at the pad bolts inner edge. The taper is actually the Tangent to the clamped shaft at the point of interest and so is only defined by the gap and the radius of the clamped bar. (I see now where my maths went wrong I used the Diameter not the radius, note to self don't do maths at bedtime).

Once the angle has been found one must just ensure that it is greater than the critical angle for the transition between self holding and self locking, given in most books as 7 degrees.

You are more than likely correct in saying there is more to taper locking as far as analysis is concerned but that is 'built in' when the transition angle of 7 degrees is taken from the literature.

The diameter of the two half nuts or pads is irrelevant as this only determines where the taper 'leaves off' at the outer end of the pad and, as this must be a greater taper angle, is of no concern.

Duncans G=D/8 certainly gets you where you want to be and if there is any tendency to fail to unlock, facing a fraction off the inner ends of the pads will easily correct it.

regards Martin

Edited By Martin Kyte on 25/06/2021 10:31:21

Edited By Martin Kyte on 25/06/2021 10:32:34

[Michael GilliganParticipant @michaelgilligan61133]

Thanks for the response, Martin

… I shall mull over that

MichaelG.

[John BaronParticipant @johnbaron31275]

Hi Guys,

The clamping angle varies very little for a given collet diameter and ultimately depends upon the diameter of the clamped part.

This drawing of a 12 mm cotter with an M6 clamping screw shows the angles for a 20 mm diameter and a 50 mm diameter shaft. The blue lines representing the collet, whilst the red lines the diameter of the clamped item. There is barely 7 degrees between them. A larger collet diameter will only make a small difference. Hardly a locking taper.

As I mentioned earlier the sharp edge on the scallop edge will cause binding and should be removed. I few swipes with a stone is enough.

[duncan webster 1Participant @duncanwebster1]

I think the angle of concern is right at the inner end of the collet, not the 'average' as drawn by JB. Whether it is a real concern I don't know, I've never managed to get one to jam, but I do have to give the quill lock on my Centec a whack wth the ball of my hand sometimes

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Martin Kyte on 25/06/2021 10:30:33:

[…]

and if there is any tendency to fail to unlock, facing a fraction off the inner ends of the pads will easily correct it.

.

I will sit back and let the discussion continue … but I admit that I am bewildered by your closing comment, Martin

Anything ‘inboard’ of the lines of contact can, as I see it, have no effect on the clamping or locking

… all that ‘facing a fraction off the inner ends of the pads’ can do is increase the gap between them.

Do please correct me if I have misunderstood your comment.

MichaelG.

[John BaronParticipant @johnbaron31275]

Hi Guys,

Michael is right, facing off the inside ends would only tend to reduce or remove the burrs that the saw or parting blade left. FWIW I just use the bandsaw to cut the collet across its centre. This usually leaves a 30 thou gap in the middle. Occasionally I face the inner ends if the cut is a bit rough.

? How about considering a split collet clamping a square cross section !

[Martin KyteParticipant @martinkyte99762]

The inner end of the pad (the gap if you like) defines the taper at that point. Removing a small portion increases the minimum taper angle and makes the pad self releasing.

regards martin

Edited By Martin Kyte on 25/06/2021 15:22:57

Edited By Martin Kyte on 25/06/2021 15:27:24

[Martin KyteParticipant @martinkyte99762]

Hi Guys,

Michael is right, facing off the inside ends would only tend to reduce or remove the burrs that the saw or parting blade left. FWIW I just use the bandsaw to cut the collet across its centre. This usually leaves a 30 thou gap in the middle. Occasionally I face the inner ends if the cut is a bit rough.

? How about considering a split collet clamping a square cross section !

 

It's not a collet it's a cotter.

regards martin

Edited By Martin Kyte on 25/06/2021 15:27:00

Edited By Martin Kyte on 25/06/2021 15:27:47

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Martin Kyte on 25/06/2021 15:20:41:

The inner end of the pad (the gap if you like) defines the taper at that point. Removing a small portion increases the minimum taper angle and makes the pad self releasing.

.

Sorry but I still don’t get it … The pads each make contact at a line ‘outside’ that area; so your increased taper cannot have any effect.

MichaelG.

[Martin KyteParticipant @martinkyte99762]

The pads have curved contact surfaces that match the main bar. There is no line contact but two matched curved surfaces as shown in Duplex's sketch (which you posted). Increasing the gap increases tha angle of the smallest part of the taper.

If the gap was almost zero then the taper angle would be very near to zero too and the pads would wedge in place.

regards Martin

I must get a drawing package, it would be so much simpler than just explaining in text.

[John BaronParticipant @johnbaron31275]

Posted by John Baron on 25/06/2021 15:19:08:

Hi Guys,

Michael is right, facing off the inside ends would only tend to reduce or remove the burrs that the saw or parting blade left. FWIW I just use the bandsaw to cut the cotter across its centre. This usually leaves a 30 thou gap in the middle. Occasionally I face the inner ends if the cut is a bit rough.

? How about considering a split cotter clamping a square cross section !

Quite right, my error !

Since it wont let me edit my original post, error corrected.

I do understand where you are going Martin, but the cotter wont work if there is no gap between the halves. So the risk of any locking is non existent. As far a CAD package is concerned, I use Qcad. The community edition is free but a perpetual licence is only £30.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Martin Kyte on 25/06/2021 16:17:54:

The pads have curved contact surfaces that match the main bar. There is no line contact but two matched curved surfaces as shown in Duplex's sketch (which you posted). Increasing the gap increases tha angle of the smallest part of the taper.

[…]

.

Sorry Martin but I continue to disagree or misunderstand

The pads should be turned to the same radius of curvature as the hole in the block [bored in-situ] which should be a sliding fit on the bar [so perhaps one thou of radial clearance] … therefore, when the pads are clamped there is only line contact between each of them and the bar.

In the Duplex drawing, these lines would be mere points, because they run into the page.

MichaelG.

.

Edit: __ if they exactly matched the bar radius then things wouldn’t slide, and there would be no need for a clamp

.

Busy doing microscopy at the moment, but I will try doing an exaggerated sketch later.

Edited By Michael Gilligan on 25/06/2021 17:58:14

[Michael GilliganParticipant @michaelgilligan61133]

As promised, Martin : Here’s my version of the clamping geometry

… with the bar shown smaller diameter, for clarity.

Assume that the bar is ‘grounded’

• Tightening the clamp screw moves the two pads
• That in turn moves the whole block sideways
• Clamping then takes place at three lines [running into the page] with locations roughly indicated by the tips of the red arrows.
• Because the clamp radius and the bore in the block are [in reality very slightly] larger than the bar radius, there can be no other contact … it’s just those three lines.

With appropriate dimensions; these movements, and the clearances created, will be small : but they do say “a miss is as good as a mile”

MichaelG.

.

Edited By Michael Gilligan on 25/06/2021 21:38:42

[david bennett 8Participant @davidbennett8]

There seems to be a bit of overthinking this wedging problem. If you accept that wedging can happen, the only place it can happen is where the clamping action is less than about 7 degrees. Eliminate that and solve the problem. It only needs a few microns of movement to cause wedging on a shallow angle and have no effect on the greater angles. The clearance on the sliding cotter/clamp bolt will allow this to happen.

Edited By david bennett 8 on 25/06/2021 23:39:30

Edited By david bennett 8 on 25/06/2021 23:41:43

[Michael GilliganParticipant @michaelgilligan61133]

Posted by david bennett 8 on 25/06/2021 23:35:41:

There seems to be a bit of overthinking this wedging problem. If you accept that wedging can happen, the only place it can happen is where the clamping action is less than about 7 degrees. Eliminate that and solve the problem. It only needs a few microns of movement to cause wedging on a shallow angle and have no effect on the greater angles. The clearance on the sliding cotter will allow this to happen.

 

.

So, please tell … how does that relate to the discussion that I am having with Martin ?

MichaelG.

.

P.S. __ personally, I would say there is just about the right amount of thinking going on.

Edited By Michael Gilligan on 25/06/2021 23:49:55

[duncan webster 1Participant @duncanwebster1]

If you draw out what happens if the bar is ever so slightly smaller than the hole, as in reality it must be or it won't go in, you will find that the curved surface of the cotter first contacts the bar at the outer end of the curved profile, so it would appear that the angle at the inner end doesn't matter.

 

Edited By duncan webster on 26/06/2021 00:38:06

[david bennett 8Participant @davidbennett8]

Posted by Michael Gilligan on 25/06/2021 23:42:24:

Posted by david bennett 8 on 25/06/2021 23:35:41:

There seems to be a bit of overthinking this wedging problem. If you accept that wedging can happen, the only place it can happen is where the clamping action is less than about 7 degrees. Eliminate that and solve the problem. It only needs a few microns of movement to cause wedging on a shallow angle and have no effect on the greater angles. The clearance on the sliding cotter will allow this to happen.

.

So, please tell … how does that relate to the discussion that I am having with Martin ?

MichaelG.

.

P.S. __ personally, I would say there is just about the right amount of thinking going on.

Edited By Michael Gilligan on 25/06/2021 23:49:55

What makes you think it was addressed to you? It was a general comment on the thread.

[david bennett 8Participant @davidbennett8]

Posted by duncan webster on 26/06/2021 00:29:02:

If you draw out what happens if the bar is ever so slightly smaller than the hole, as in reality it must be or it won't go in, you will find that the curved surface of the cotter first contacts the bar at the outer end of the curved profile, so it would appear that the angle at the inner end doesn't matter.

Edited By duncan webster on 26/06/2021 00:38:06

I do not agree. The curved surface will contact both ends of the curved profile at the same time. Then the curve will force the sliding cotter around the bar and into a wedging action at the bottom.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by david bennett 8 on 26/06/2021 01:24:46:

.

What makes you think it was addressed to you? It was a general comment on the thread.

.

Only the fact that it immediately followed my post.

Thanks for the clarification

MichaelG.

Edited By Michael Gilligan on 26/06/2021 06:24:01

[John BaronParticipant @johnbaron31275]

Good Morning Guys,

I understand both points of view !

Only if one side of the cotter is longer than the other could there be any possibility of wedging, this could happen if the cotter were cut off centre or the cotter was a very loose fit.

Since a cut in the centre of the cotter would remove material and make both halves shorter by equal amounts the very fine taper on each would be removed.

Any burr on the cut edges will dig into the shaft being clamped and cause sticking and shaft damage so it must be removed.

I agree that the cotter provides a linear clamping action rather than a wedging one ! However as shown in the diagram that Michael posted the red arrows showing the force direction that will be directed at the back of the bore that the cotter slides in.

[CirclipParticipant @circlip]

Wonder if there's a formulae to determine the spacing required between a posting and reply to ensure a navel contemplation as opposed to a posterior verbalisation without a hint of paranoia?

Regards Ian

[Author]

Posts