Retro Computing (on Steroids)

[Gerard O’TooleParticipant @gerardotoole60348]

Sorry if it a bit off topic, but i haven't seen any mention of Forth.

I remember a small computer, similar in every way, except colour, to the Sinclair. I think it was called the Jupiter Ace.

My reason for mentioning is that it would seem an ideal language for CNC etc and for a lot of what we do in workshop.

Just wonder if anyone here uses it or has any up to date information?

[SillyOldDufferModerator @sillyoldduffer]

Posted by Gerard O'Toole on 15/12/2020 09:38:37:

Sorry if it a bit off topic, but i haven't seen any mention of Forth.

…

Just wonder if anyone here uses it or has any up to date information?

Not in modern times, but I used Fig-Forth on my Nascom-1, an early Z80 microcomputer. By modern standards the Z80 is a slow CPU, and memory was tiny and gob-smacklingly expensive. Off the shelf, the Nascom was programmed manually in HEX, so developing the smallest program took forever. Then a 2kB ROM TinyBASIC appeared, which was much easier to use, but had severe restrictions. Fitting 16kB of RAM opened the door to an Assembler (Zeap), and after a year or two, a Microsoft-like BASIC appeared. Zeap did most of what I wanted, but writing Assembly Language is hard work so I was always looking for a decent small compiler. C and PASCAL were too big for the machine (it needed 32kB RAM and a disc), but Forth met the bill.

Lots of nice things about Forth – moderately high-level, compact, extensible, and fast. I believe it was used control the cameras and other special equipment that created special effects for the original Star Wars films, which led to it being used today to control astronomical telescopes, and for some embedded applications.

My main problem with Forth is the need to think in Reverse Polish Notation. The programmer has to push & pop commands and data on and off a stack, which isn't how I think. For example:

• BASIC:     LET A = 2 + 3
• C:            A = 2 + 3;
• FORTH:   3 2 +

From this tutorial, most languages do IF condition like this:

IF        Decide flag value of 'cold'.
 cold     Formulate flag
THEN      Leave construct when flag=false
 coat-on  Conditionally executed code
ENDIF     End

In Forth this is written:

( cold?     flag on stack )
IF          On 'false', jump to THEN
 coat-on    Conditionally executed code
THEN        End; could be named ENDIF

Later, when home computers became powerful enough to run C, PASCAL, editors and IDE's etc, I abandoned Forth. C is 'better' for low-level stuff, and high-level languages like BASIC are easier to write. Forth is still used, but it's not generally popular.

Dave

Edited By SillyOldDuffer on 15/12/2020 10:49:28

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Gerard O'Toole on 15/12/2020 09:38:37:

Sorry if it a bit off topic, but i haven't seen any mention of Forth.

[…]

Just wonder if anyone here uses it or has any up to date information?

.

There’s an App for that ^^^

**LINK**

https://apps.apple.com/gb/app/retro-forth/id1170943580

MichaelG.

[IanTParticipant @iant]

We seem to have a lot of common background SoD

All this talk of Nascom, Zeap and now Forth. It took me forever to type Fig-Forth into my Nascom system and to then find all my typos and get it working – but it was really the only way to get my graphics card (based on a TI chip) running in a usable way.

I've managed not to mention Forth here (thus far) but for control/embedded uses, I would suggest that folk look at MeCrisp & MeCrisp-Stellaris by Matthias Koch. I have it running on STM "Blue Pill" boards which may have been replaced by newer products these days but could be had for about £3 – very reasonable for a complete RTR STM32 board.

MeCrisp Forth

Forth is a threaded (stack-based) language and RPN is one of the side effects of using a stack to perform everything. I think the simplest (& maybe best way) to describe Forth – is that it is extremely useful to write other 'application-specific' languages with. So if you need a robot-control language, a plain-language to G-code parser, a telescope user interface – Forth will let you write a programme that uses application appropriate wording/commands – e.g. "Left Arm 22 mm Up" or " Traverse Head To Home" or "Track X Y Z Co-Ord From Set Time" where each 'word' (Left, Arm, Head, Set) can be thought of as a sub-routine that is executed.

I won't bother to further explain it here (like BASIC most programmers seem to hate Forth btw!) but if you would like to know more about MeCrisp (Forth) then have a browse here…

MeCrisp (unofficial) Doumentation

Regards,

IanT

[Another JohnSParticipant @anotherjohns]

Dear SOD;

Sure, Python's great, I use it a bit at work. However, I have to use C99; Shader work and OpenCL Kernels require this. (have to run on older code platforms sometimes, sticking to OpenCL, OpenGL for the moment)

Your request is tailored to using a language like Python; if I reworded it to something like "find ALL the palindromes in the set [0->2,147,483,647] and return a flag indicating which one is set" then I'd win hands-down, especially with a good graphics card.

BR – JohnS.

[IanTParticipant @iant]

SoD – having said I wasn't a Computer Science bod – you went ahead and set what I suspect would be an exercise for first year Computer Science Grads – who presumably have been introduced to "SoDs Algorithm" or some such as part of their course !

Your problem is clearly not a simple as it might first appear but by 'Trial and Error' I did manage to get a "Bucket" approach working (no bounds checking or anything) but clearly this wouldn't scale for the problem you described. This programme took me about 30-40 minutes (the next day) over coffee and whilst it might not impress a programmer – I was quite pleased getting this far from scratch. A T&E approach is very simple (and fast) to do with MMB – so it suits a programming 'dummy' (like myself) who is trying to work things out as they go along.

'
' Numeric Palidrome 091220/1
'
OPTION EXPLICIT
OPTION DEFAULT NONE
'
CLS
DIM N%, L1%, M1%, H1%
INPUT "Input seed number"; N%
'
L1% = N% MOD 10
M1% = ((N% MOD 100) – L1%)/10
H1% = ((N% – L1% – (M1%*10)) MOD 1000)/100
'
PRINT L1%, M1%, H1%
END

I now have newer programmes that use more iterative processes and that I will (eventually) get to work – but it's very much my Christmas Crossword Puzzle – so I have a go at it when I have a quite moment and feel in the mood (which as Christmas gets nearer is harder to do).

Regards,

IanT

PS Should have illustrated Forth with classic example code (for a washing machine) " Rinse Wash Drain Dry "

Edited By IanT on 15/12/2020 11:58:32

[BazyleParticipant @bazyle]

I wonder if anyone still has a working PET.

[Gerard O’TooleParticipant @gerardotoole60348]

Thanks, Dave, Ian, Michael, John for the information and links to Forth.

It was the "Retro Computing

" title that got me thinking about Forth. I had a Jupiter Ace and I also had Forth on a HP 85 Computer. I enjoyed playing around with it but at that time the need was for large data programs and Pascal took up most of my time. I can't pretend to have ever coded any serious application but I still have the 'Starting Forth' book.

Now that I am retired , I want to play around with Arduino and motor control with a view to CNC at some time. Forth just seemed ideal, given it was developed to control large astrological Telescopes . It was also very memory efficient. I know the HP computer came with 16K memory, 2.2Mb 8" disks (which were considered huge at the time)and memory was always an issue with every program.

I wil check out the links and hopefully get started somehow.

Thanks

PS. Still have the HP computer – it was dumped and I literally rescued it from a skip. Not sure what happened to the Ace

[Robert Atkinson 2Participant @robertatkinson2]

If you find the ACE, they sell for around £500 on ebay.

[IanTParticipant @iant]

'Starting Forth' by Leo Brodie – the classic intro book for learning Forth. Can be found here as a PDF or online version. The illustrations really help to understand stack manipulation in an amusing way.

Starting Forth – Leo Brodie

Regards,

IanT

[Michael GilliganParticipant @michaelgilligan61133]

Almost incredibly:

I have just stumbled across my paper copy of FORTHWRITE issue 55, datedAugust 1990

This was published by FIGUK … the FORTH Interest Group(UK)

No idea if they ever made it to the Internet.

MichaelG.

[IanTParticipant @iant]

Posted by Michael Gilligan on 15/12/2020 13:36:03:

Almost incredibly:

I have just stumbled across my paper copy of FORTHWRITE issue 55, datedAugust 1990

This was published by FIGUK … the FORTH Interest Group(UK)

No idea if they ever made it to the Internet.

MichaelG.

I don't know about 'Forthwrite' Michael – but the US version (Forth Dimensions) certainly was archived. I haven't managed to find the site I originally downloaded my copies from (it was some time ago now) which was sorted by volume. There are some FD editions available at the site below – although they seem somewhat randomly ordered.

Forth Dimensions

Regards,

IanT

[Frances IoMParticipant @francesiom58905]

IanT – no you are merely using the wrong projection – try title!

[SillyOldDufferModerator @sillyoldduffer]

Posted by IanT on 15/12/2020 11:54:32:

SoD – having said I wasn't a Computer Science bod – you went ahead and set what I suspect would be an exercise for first year Computer Science Grads – who presumably have been introduced to "SoDs Algorithm" or some such as part of their course !

…

Not so, the challenge is from Creative Computing magazine circa 1976, almost all of which was BASIC! This one is more number theory than computer science, but the problem isn't that unusual – data getting bigger and bigger!

Here's an answer from the time:

And then this more sophisticated version:

I suspect it would be a challenge to get these working today, because both are written in – I think – minicomputer dialects, not the tidied up BASICs we're used to. For example, Tom Karzes' BASIC appears to allow him to use 'b' as both a scalar integer and as an array, while Gregory Yob had an interpreter that could add strings numerically, eg A$ = "123"
B$ = "321"
so A$ + B$ is "444"

Today most BASICs do string concatenation, eg A$ + B$ is "123321"

No disrespect to Tom Karzes, but his program demonstrates why classic BASIC fell into disrepute. No obvious structure, meaningless names, GOTOs, plus noisy line numbers and continuations. Hard to understand how his code works.

Gregory Yob's program contains a showstopper. DIM A$(254) is the maximum number of digits his BASIC could store in a string. Far too small – after only 1000 reversals '196' is over 400 digits long:

353466443924136897858377144029121143628590980834140834402086145040599291832845719034956
387168795800463971545914548326676428378028814710683108505496412733883652599320082374934
620554240912515790120016687692352197776621010107415220132544026439582289914006246477437
313605494900387117318730883824675524836409655069474008586970693559441817449338082995150
442581194537942329079105826441012030342772858788740429334664452

For the same reason, it's not amenable to John Alexander Stewart's "find ALL the palindromes in the set [0->2,147,483,647] and return a flag indicating which one is set". I like the idea of using a graphics card, but am confident it won't prove 196 never becomes palindromic because 196 is a Lychrel Number – it's 'an unsolved problem in mathematics'. Wikipedia says the reversal number has been taken to over billion digits without becoming a palindrome.

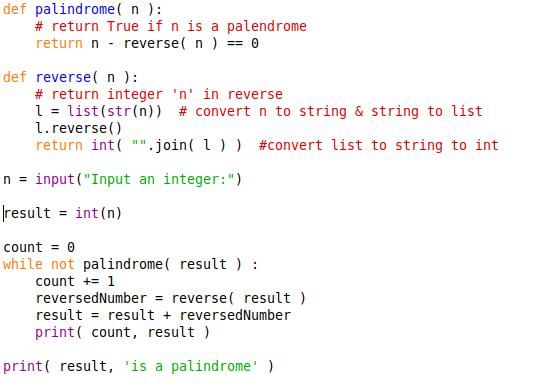
Python can't do a billion digits on my machine but I submit it makes the logic of my working version clearer, and it handles big numbers gracefully:

Python3 strings and integers are only limited by the amount of machine memory available. Although there's no Python command to reverse a string in place, reversing lists is built in, and it's trivial to convert strings to lists and vice versa. Lists might seem like an arcane computer science structure, but they're not!

Micromites are marvellous compared with the computers available in 1976, be interesting to see how far one could get with the 196 palindrome problem.

Dave

[Frances IoMParticipant @francesiom58905]

the key is structure used to hold numbers – which can be generalised to any radix – you hold then as a sequenced set of digit tokens for which a definition of addition is a wraparound index on this set which wraparound sets a carry in a second string – a number is I think a palindrome when the addition of two sequences of digit strings added in reverse direction produces no overflow – by this you could easily program hexadecimal palindromes etc

[SillyOldDufferModerator @sillyoldduffer]

Posted by Frances IoM on 15/12/2020 16:56:30:
the key is structure used to hold numbers – which can be generalised to any radix – you hold then as a sequenced set of digit tokens for which a definition of addition is a wraparound index on this set which wraparound sets a carry in a second string – a number is I think a palindrome when the addition of two sequences of digit strings added in reverse direction produces no overflow – by this you could easily program hexadecimal palindromes etc

Can you give an example please Frances? I'm OK ( I hope!) up to: for which a definition of addition is a wraparound index on this set. My maths is limited, and you just popped the fuse!

Dave

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Michael Gilligan on 15/12/2020 13:36:03:

[…]

No idea if they ever made it to the Internet.

.

’ere we go … **LINK**

http://www.figuk.plus.com/articles.htm

MichaelG.

[Frances IoMParticipant @francesiom58905]

dave think about palindromes of octal number the set is 0,1,2,3,4,5,6,7 to add 4 to 2 move the index from 2(assuming set starts from index 0) then move 4 positions, adding 6 to 2 will wrap around in set thus triggering a carry
thus the structures needed are (n,array of digits[index set 0..n-1) – adding 2 of these structures needs n to be equal (if not a copy into a larger array is needed) – the carry array is always on size n+1 and may have 1 in several positions this if carry set not all zero first extend the addition to size n+1 + add carry and repeat whilst carry set not all 0.

[IanTParticipant @iant]

Posted by Frances IoM on 15/12/2020 18:16:56:
dave think about palindromes of octal number the set is 0,1,2,3,4,5,6,7 to add 4 to 2 move the index from 2(assuming set starts from index 0) then move 4 positions, adding 6 to 2 will wrap around in set thus triggering a carry
thus the structures needed are (n,array of digits[index set 0..n-1) – adding 2 of these structures needs n to be equal (if not a copy into a larger array is needed) – the carry array is always on size n+1 and may have 1 in several positions this if carry set not all zero first extend the addition to size n+1 + add carry and repeat whilst carry set not all 0.

'Octal' Frances? I used to know that a long time ago – but all I can remember now is '7402' (Halt instruction on a PDP8)

IanT

[Frances IoMParticipant @francesiom58905]

IanT – I’m old – Honeywell 316 + 516s – one of my home computers is in the Science museum collection (long story but one of the first UK built machines – 68008 based running a variant of Unix in the late70s)

[Gerard O’TooleParticipant @gerardotoole60348]

Posted by IanT on 15/12/2020 13:03:35:

'Starting Forth' by Leo Brodie – the classic intro book for learning Forth. Can be found here as a PDF or online version. The illustrations really help to understand stack manipulation in an amusing way.

Starting Forth – Leo Brodie

Regards,

IanT

I just found my old copy. A bit battered but all there.

Now to see if i can make any sense of it

[Gerard O’TooleParticipant @gerardotoole60348]

Not as concise as Python but works . ( C#)

On 196 problem , the highest integer before crashing was was 7197636720180367016 , using Int64 and highest value using Int32 is set at 2,147,483,647

I was surprised at the number of integers which became palindrome after only one loop.

[SillyOldDufferModerator @sillyoldduffer]

Posted by Gerard O'Toole on 16/12/2020 16:34:39:

…

On 196 problem , the highest integer before crashing was was 7197636720180367016 , using Int64 and highest value using Int32 is set at 2,147,483,647

I was surprised at the number of integers which became palindrome after only one loop.

Looks good to me, and I think it can be souped up. Never done C# myself, but I believe C# strings can be longer than telephone lines while BigInteger does arbitrarily big arithmetic. Maybe simply substituting BigInteger for Int32 in your declarations will allow the program to generate monster numbers?

After working out how to reverse and add huge numbers the next challenge is to it efficiently which my attempt isn't. Your C# program is likely faster than mine because C# reverses strings directly, whereas I convert between lists and strings, an awful spiralling overhead as the number of digits grows.

Most numbers quickly become palindromic, some take many reversed additions before a palindrome appears, and a few – like 196 – might never produce a palindrome. No one knows! Mathematicians find it an interesting problem, I think it's a good way of stressing computer languages.

Dave

[Frances IoMParticipant @francesiom58905]

Dave – I pointed out that you never treat as ‘integer’s of any size but always treat as a string of ‘digits’ of whatever radix you want to play with – one simple approach is to use a struct (length,array[max length]) and add in place

[SillyOldDufferModerator @sillyoldduffer]

Posted by Frances IoM on 16/12/2020 17:52:25:
Dave – I pointed out that you never treat as 'integer's of any size but always treat as a string of 'digits' of whatever radix you want to play with – one simple approach is to use a struct (length,array[max length]) and add in place

I'm on the case Frances! My comment about Gerard's program is separate. Just that by replacing his Int32 with BigInteger declarations I think it will do big numbers!

I'm musing on how best to code your method: a c++ class (struct on steroids!) feels right, probably with a vector rather than array so it can grow.

Dave

[Author]

Posts