Posted by John Haine on 01/03/2023 09:34:14:
Posted by Mason Green on 28/02/2023 23:23:58:
Posted by John Haine on 28/02/2023 10:27:08:
…
…
Essentially over a long period of time the pendulum is self-correcting despite the random forces acting on it.
–MG
…
I'm not sure to what a pendulum clock can "self correct" over a long term. At any instant it has a state completely determined by its history and what happens next depends on that state and how its environment behaves.
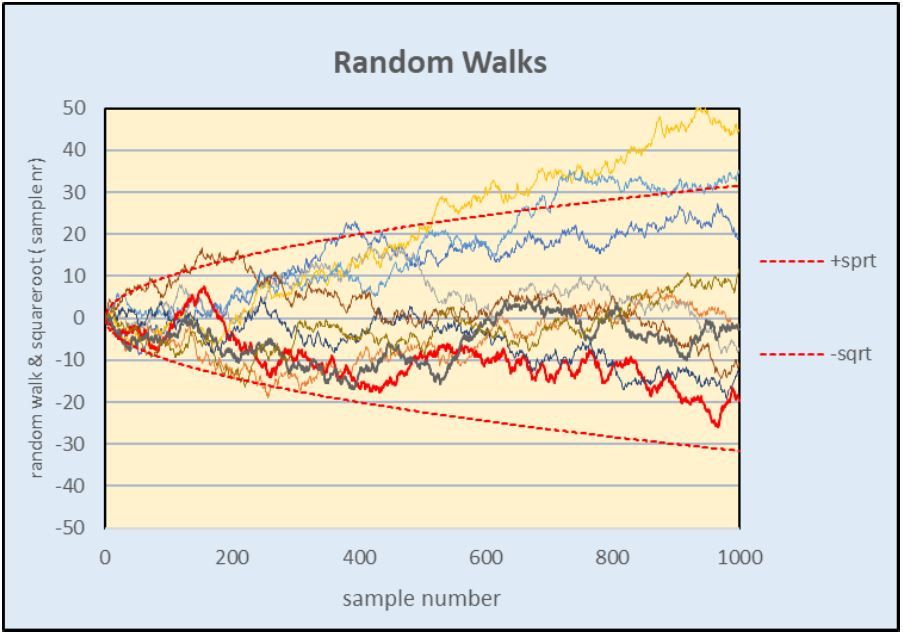
I understood Mason's comment to mean that pendulum period varies as it responds to changes in the environment, which can be compensated for, but also randomly, resulting in noise. A pendulum "self-corrects" in the the sense that many instabilities cancel out on average.
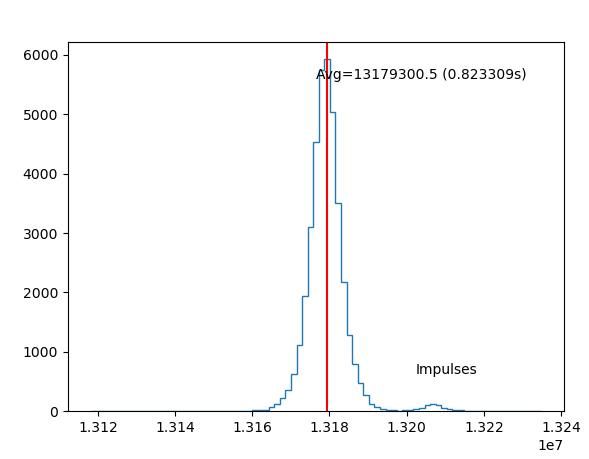
A 1 second mechanical pendulum, no matter how well made, does not deliver exact 1 second periods. Periods are always slightly different, but cluster around a median, like this example from my clock. The vast majority of beats are near the median, but a proportion are distributed either side, with extreme variations becoming increasingly rare. The steeper the peak the better – high Q – but, even if the pendulum is fully compensated, there is always some variation, or noise. Any frequency that''s not exactly average is noisy.
 .
.
On average, the pendulum keeps time, but the period of individual beats vary. Deviations to the right tend to balance out deviations to the left over time. A well-made pendulum delivers good long-term stability by averaging out noise, even though the pendulum's short-term stability could be relatively poor.
Nonetheless, it's desirable to improve short-term stability as well. As I understand it Allan deviation measures and identifies the types of noise, so it might be possible to reduce or engineer them out. Worrying about noise is precision clock territory! An example: Invar is an Iron/Nickel alloy that doesn't change size as temperature varies. It's excellent for making pendulum rods. But looking closely at Invar rod clock performance shows Invar is far from perfect! When measured at high resolution, it turns out Invar is unstable at the molecular level, causing minute physical changes that change the pendulums period slightly. The instability can be reduced by heat ageing, but Invar isn't perfect, and maybe another material like quartz, might do better. But fundamentally, everything the clock is made of is a bit unstable.
Therefore, I don't agree with John's: "At any instant it has a state completely determined by its history and what happens next depends on that state and how its environment behaves". However the difference of opinion is tiny, because my version is: "At any instant it has a state almost entirely determined by its history and what happens next depends on that state and how its environment behaves"
Dave
Edited By SillyOldDuffer on 01/03/2023 11:35:05
John Haine.