Parting Off MEW225

[Michael GilliganParticipant @michaelgilligan61133]

Posted by blowlamp on 16/02/2015 13:09:43:

I've tweaked it a bit to make my additions a little clearer.

.

Sorry, Martin, I can't see the change.

These are the words I had in mind: " carbide insert tool, preferably with positive rake geometry designed for smaller lathes & gentle cutting forces"

MichaelG.

[Hamish McNabParticipant @hamishmcnab62554]

As a total beginner I find parting off a very scary experience and will admit I am not able to comprehend much of the previous tech speak. As a "model engineer" and only doing the occasional cut so not needing all the technical in and outs and finding using a hacksaw tedious I decided to look at another way. Not rocket science and no doubt done before but I made a bracket for my angle grinder, mounted on the tool post and with a thin cutting disc it went cut like a hot knife through butter and surprisingly little mess.

Parting off is not a problem now. Instead of a disc could I use a blade?

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Hamish McNab on 16/02/2015 15:43:41:

… I made a bracket for my angle grinder, mounted on the tool post and with a thin cutting disc it went cut like a hot knife through butter and surprisingly little mess.

Parting off is not a problem now. Instead of a disc could I use a blade?

.

Hamish,

You may be onto something there; but two big caveats …

1. The dust from a grinding disc is likely to be very abrasive, and I wouldn't want to risk it on my lathe.
2. Some sort of slitting saw blade would seem more appropriate … but would need to be run much slower than Angle Grinder speed [which is circa 14,000 rpm if I recall correctly].

MichaelG.

Edited By Michael Gilligan on 16/02/2015 15:55:47

[Russell EberhardtParticipant @russelleberhardt48058]

Posted by Michael Gilligan on 16/02/2015 09:24:47:

As indicated … I do not "have the maths" but:

I'm forgetting my maths as well. I should have said that "The Q is proportional to the ratio of energy stored in the resonant system to the energy lost per cycle." There is a factor of 2 x Pi in there somewhere.

Russell.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by blowlamp on 16/02/2015 11:09:56:

It seems to me that the Swan-neck tool is meant as a kind of safety valve in the event of a lock-up occurring.

.

Martin,

That's an interesting interpretation: You may be right, but most of the examples I have seen were promoted as anti-chatter or as providing better surface finish. … The distinction between this and "meant as a kind of safety valve in the event of a lock-up occurring" may, of course, be too subtle to worry about.

MichaelG.

[Gordon WParticipant @gordonw]

I also use an angle grinder for most cutting, but not on the lathe A thought for all you tech. and maths wizards- has anyone tried damping the cut-off blade ? I'm thinking wrapping a piece of lead sheet round the blade holder, if possible. I know this helps with boring bars.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Gordon W on 16/02/2015 16:22:55:

… has anyone tried damping the cut-off blade ? I'm thinking wrapping a piece of lead sheet round the blade holder, if possible. I know this helps with boring bars.

.

Strange as it may seem, Gordon; BlueTack is remarkably good for local damping.

It's an extraordinary material, worthy of much more serious use than sticking posters up.

MichaelG.

Edited By Michael Gilligan on 16/02/2015 16:32:41

[Hamish McNabParticipant @hamishmcnab62554]

Posted by Michael Gilligan on 16/02/2015 15:54:13:

Posted by Hamish McNab on 16/02/2015 15:43:41:

… I made a bracket for my angle grinder, mounted on the tool post and with a thin cutting disc it went cut like a hot knife through butter and surprisingly little mess.

Parting off is not a problem now. Instead of a disc could I use a blade?

.

Hamish,

You may be onto something there; but two big caveats …

1. The dust from a grinding disc is likely to be very abrasive, and I wouldn't want to risk it on my lathe.
2. Some sort of slitting saw blade would seem more appropriate … but would need to be run much slower than Angle Grinder speed [which is circa 14,000 rpm if I recall correctly].

MichaelG.

Edited By Michael Gilligan on 16/02/2015 15:55:47

I thank you for your advice. The amount of dust created was minuscule and cleaned off soon after and I doubt if it would have any affect on the lathe. Is there any evidence of damage being caused to a modellers lathe by grinding?

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Hamish McNab on 16/02/2015 17:36:59:

Is there any evidence of damage being caused to a modellers lathe by grinding?

.

Well … I'm sure that other members will have their stories, good and bad … but here is mine:

Many years ago, I bought an old lathe, which I then found to be "hollow" over the length of the bed by about 15 thou'.

The previous owner had used it for sharpening LawnMower Blades.

I learned my lesson.

MichaelG.

[Hamish McNabParticipant @hamishmcnab62554]

Posted by Michael Gilligan on 16/02/2015 17:49:58:

Posted by Hamish McNab on 16/02/2015 17:36:59:

Is there any evidence of damage being caused to a modellers lathe by grinding?

.

Well … I'm sure that other members will have their stories, good and bad … but here is mine:

Many years ago, I bought an old lathe, which I then found to be "hollow" over the length of the bed by about 15 thou'.

The previous owner had used it for sharpening LawnMower Blades.

I learned my lesson.

MichaelG.

Again I thank you for your information. As I emphasised I was relating to a modellers lathe and not one used for commercial purposes. I will be interested to hear other "stories".

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Hamish McNab on 16/02/2015 18:33:20:

I will be interested to hear other "stories".

.

… Over to you, Chaps !!

MichaelG.

[WALLACEParticipant @wallace]

I haven’t thought about it too much … but… I wonder if some of the ‘angst’ with parting off with a Myford is due to it being a plain lathe I.e. without prismatic guides ?

Would the various resultant forces on the tool post when parting off be any different with or without them ?

W.

[Bob Brown 1Participant @bobbrown1]

I personal think one of the issues with parting off is back lash in the cross slide, even a relatively small amount of back lash could cause the tool to grab the work piece such that the tool is over loaded and cause it to break, a bit like climb milling.

Top rake on the tool will have a tendency to pull the tool into the work piece and break the tool.

Bob

[Chris TriceParticipant @christrice43267]

I made that very point Bob.

[Bob Brown 1Participant @bobbrown1]

Chris,

Just thought it was worth making it again, I have had the situation where the tool has grabbed the work piece when parting aluminium and snapped the tool. On inspection it can be seen that the cause was the tool being pulled into the work piece as the depth of cut has become excessive, it is not down to build up on the tool tip as there is no sign of welding of the material to the tool tip. I wonder how much back lash people have in there cross slide, easy to measure with a clock gauge, mine is 0.006" with no adjustment in the nut.

Bob

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Hamish McNab on 16/02/2015 18:33:20:

Posted by Hamish McNab on 16/02/2015 17:36:59:

Is there any evidence of damage being caused to a modellers lathe by grinding?

.

I will be interested to hear other "stories".

.

Hamish,

In the absence of any endorsement of my advice, by others: It looks like you are on your own.

Note: It may be worth re-stating your question on a fresh thread, as I doubt that everyone is reading this.

MichaelG.

[Hamish McNabParticipant @hamishmcnab62554]

I appreciate your comments and it is only for interest that I posted.

With reference to your own experience, was the hollow created by the the grinding residue or by the constant use of machining in the same position?

I am here to learn.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Hamish McNab on 17/02/2015 09:09:06:

With reference to your own experience, was the hollow created by the the grinding residue or by the constant use of machining in the same position?

.

It's about forty years ago, so recall may not be precise, but I think the previous owner was sharpening his own cylinder mower blade [and probably a few for others in the village] rather than it being a mass-market operation.

The cylinder was held between centres and a toolpost grinder traversed the bed whilst the cylinder was rotated to get the helix. … sorry, don't know if this was geared [like screwcutting] or manual rotation.

MichaelG.

[Russell EberhardtParticipant @russelleberhardt48058]

Posted by Bob Brown 1 on 17/02/2015 07:58:44:

I have had the situation where the tool has grabbed the work piece when parting aluminium and snapped the tool.

Try reducing the top rake on the tool?

Russell.

[MuzzerParticipant @muzzer]

At one time (when I was at school) I did up lawnmowers to make a few quid so I could buy tools and run my first car. Sharpening cylinder mowers doesn't require you to take the machine apart. You simply apply the grinding paste to the blades and tighten them against the straight blade with the machine running (or stop it between adjustments if anybody is watching). Takes minutes (you need to clean it up afterwards) and feeding a sheet of newspaper into the blades afterwards confirms that / if you have done a good job of it. I used to be able to cut said single sheet cleanly while rotating the blades by hand slowly. Apart from a handful of models, lawnmowers really weren't designed to be taken apart for sharpening although there's no law against wasting your life away.

Murray

[Anonymous]

Posted by Bob Brown 1 on 17/02/2015 07:58:44:

I wonder how much back lash people have in there cross slide, easy to measure with a clock gauge, mine is 0.006" with no adjustment in the nut.

About 0.008", I suppose I ought to adjust the nuts. My cross slide can be pushed back and forth by hand, but I have never had a tool 'grab' and pull in. On my repetition lathe the cross slide is hand operated, no leadscrew. I have parted off hundreds of aluminium components and never felt the tool (HSS) pulling in.

Andrew

[Anonymous]

Posted by Neil Wyatt on 16/02/2015 12:57:26:

Parting is such sweet sorrow that I’ll keep trying until tonight becomes tomorrow

It didn't do Juliet any good though did it!

Andrew

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Muzzer on 17/02/2015 09:59:00:

Sharpening cylinder mowers doesn't require you to take the machine apart. You simply apply the grinding paste to the blades and tighten them against the straight blade with the machine running (or stop it between adjustments if anybody is watching). …

Apart from a handful of models, lawnmowers really weren't designed to be taken apart for sharpening although there's no law against wasting your life away.

.

That's useful to know, Murray … But my man was working on 'hand push' mowers [which might make your process a little trickier].

MichaelG.

.

Now, I suppose we should get this thread back on topic.

[CabengParticipant @cabeng]

How do I get past this mental block about the direction of forces on the tool tip? OK, let’s see if this works: this link will take you to Sandvik’s home page.

**LINK**

Click on the ‘Knowledge’ tab, at the bottom of the next screen you’ll see a globe, scroll down to ‘register for our free e-learning…’ and click on that – you won’t need to register. Next page click ‘Introduction’ in the left panel, click the yellow ‘Training Manual’ panel to down load the manual.

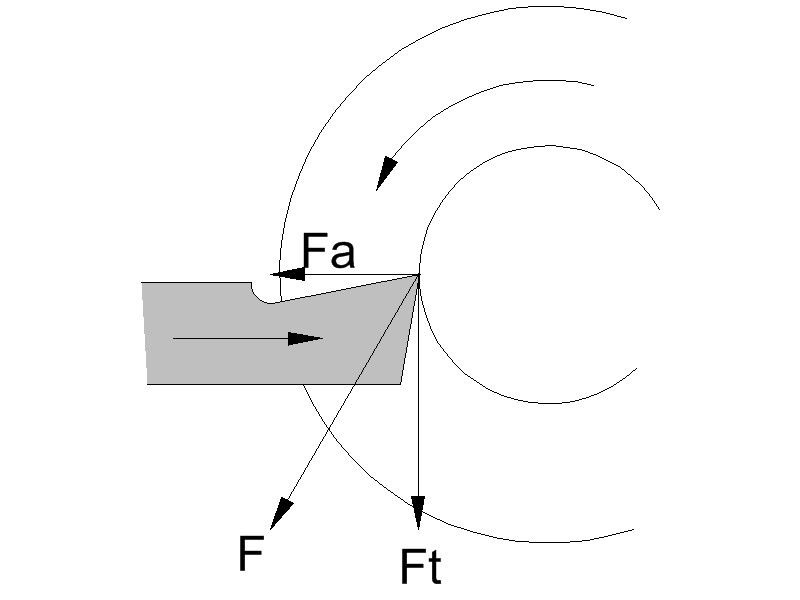
When you go into the downloaded zip file, open MCT.pdf and scroll through to page A57, where you will find a diagram of forces acting on the tip of a boring tool (for some reason they don’t show the forces on an external tool anywhere that I can find, so you’ll have to imagine what it would be like). Note how the forces are directed – tangential force Ft perpendicularly down, feed force Fa, opposite way to the feed direction, and radial force Fr, AWAY from the work surface, it is not directed into the work surface.

Now think parting tool on the outside – the forces will be directed in the same directions relative to the tip of the tool, so we end up with:

Fr isn’t present now, it’s effectively part of Fa. F is the resultant force on the tool tip, down and out, exactly as I showed it.

The hardness of the material, in conjunction with the feed rate and depth of cut, determine the relative magnitudes of Fa and Ft, and therefore the magnitude and direction of F…oh look, another sketch…

HEALTH WARNING: much simplified re the forces at the tool tip, intended only to be illustrative, and to get your thinking into a different mode!

Sketches show a single tooth hacksaw blade sitting on a piece of mild steel, A. At B, you push the blade forward only, it does not cut. Similarly at C, you push downwards only – again, it does not cut.

Since you’re pushing, you’re exerting a force, so the arrows also show the direction of the force, with the length of the arrows representing the magnitude of the force that your applying. More force, longer arrow.

At D you’re pushing along and in, it cuts. The resultant of the along and down forces is the angled arrow pointing down and to the right. At E, the forces are moved to the cutting edge, as that’s where they are being applied.

As my good friend Isaac pointed out in 1687, every action has an equal and opposite reaction, so as the tip pushes down on the steel, the steel pushes back on the tip with the same magnitude and direction, F.

G – I is a softer material (e.g. aluminium), less down force needed, so the down arrow is shorter, the resultant is shorter and at a reduced angle, as is the reaction force on the tip.

J – L are for a harder material (stainless steel?), more down force needed to push the blade into the cut, reaction force on the tip is larger, but this time at an increased angle to the surface being cut.

G – I could also represent steel with a shallower depth of cut, J – L steel with an increased depth of cut.

Note that Sandvik make no comment with regard to any possibility of arriving at a force that would drag the tool into the work, surely they would have done so had it had the potential to cause disaster? The Training Manual mentions with all sorts of machining problems, so why ignore that one, if it exists? Or perhaps it’s because they never, in their wildest dreams, thought anyone would try to cut brass with a tip designed for aluminium, as Chris did? (Sorry Chris, I couldn’t resist that one!)

Back to the boring tool – can you think of anything that would better demonstrate that there isn’t any force trying to pull the tool in to the work? If there were such a force, wouldn’t the boring bar (probably the most flexible tool in our armoury) get pulled in? It would indeed get pulled in, and viciously. And if somehow it were to be pulled in in a ‘non-vicious’ manner, it would bore oversize. But that doesn’t happen, if anything, it bores undersize – it gets pushed OUT, so that we have to ‘work the spring out of the tool’ to get the bore to size. So the boring tool also demonstrates that the force is ‘out’ and not ‘in’.

Oh yes, another point about the boring tool system – the downward force Ft tends to INCREASE the depth of cut as it pushes the tool down, which would be a perfect situation for dig in to occur, if the tool were not being pushed out of the work. And not only is it pushed out, but as you can see from the diagrams above, the deeper cut results in more force pushing the tool out. Hence, no dig in.

How does that float yer boat?

[Mark CParticipant @markc]

I doubt Sandvik considered their discussion would be used to describe what happens on rubber lathes like most of ours (read, elastic or nonrigid like industrial machines). On small diameters the tool tip height gets exponentially more critical and any tendency for compression of the tool tip point (in space) relative to any "lift" in the work due to movement in the chuck/lathe head stock assembly will generate a relative lowering of the tip height and potentially a force dragging the tool into self feed mode. At some time or another I would expect most people have got carried away with the feed rate (particularly in feed) and had the tool "dive" under the work, I have and I generally like to make certain the chuck is tight but it didn't stop me breaking the end of the parting tool where it supports the tip and then part ejecting the work before the motor stalled – and I have a Boxford so it is no toy.

If I can find the time to finish preparing the simulation I will get it done and see what moves and by how much (in theory)

Mark

[Author]

Posts