Model Turbines

[Turbine GuyParticipant @turbineguy]

The following chart shows the updated performance described in the preceding post The values for running with air should be good estimates. I cannot verify the powers shown for the testing on steam but believe they should be reasonably accurate.

[Turbine GuyParticipant @turbineguy]

The testing of the very small propellers can be greatly affected by friction and flow blockage. The following picture shows the large portion of the propellers flow area that is blocked by the relatively large rotor housing. Since the propeller is only about 0.4in. (10mm) away from the housing, the effects of flow blockage might be substantial. I did more research on the effects of Reynolds number and found most other sources showed much less effect than I was calculating using Dr. Balje’s guidelines. Dr. Balje in his summary stated the Reynolds number effects should be minimal for most turbines, so I don’t think I am estimating them correctly. Because of these concerns, I tried another way to estimate the power that will be shown in the next post.

[Jens Eirik Skogstad 1Participant @jenseirikskogstad1]

Although the horsepower is not high, the horsepower / torque will increase at the reduced speed via the gearbox.See at my steam turbine in this link..

Model steam turbine with 79 mm 4 blade propeller. **LINK**

Model steam turbine with Graupner 65 mm 2 blade propeller (in fault rotation direction)  **LINK**

Edited By Jens Eirik Skogstad on 21/12/2019 13:32:01

[Turbine GuyParticipant @turbineguy]

The following picture shows the setup I used to find the stall torque of my turbine 3. I used a 3/8 oz. fishing jig as a weight. To confirm that the weight of the jig was correct, I measured the jig and used the lengths, diameters, and densities of the steel hook and lead to calculate the weight. The calculated weight was 0.38 oz. I held the propeller in the horizontal position, placed the jig on the propeller in the approximate position shown, and turned on my airbrush compressor. I then moved the jig to a position that it could keep the propeller from rotating when I removed my hand. Next, I moved the propeller by hand to where the left side was slightly above and then slightly below the horizontal position. The jig could hold the propeller from turning in all three positions with the full air pressure of 24 psig. The picture below was taken in the last position tried. The distance from the center of the turbine to the point of contact of the jig on the propeller was 0.54 in. in all three positions of the propeller. The stall torque is 0.54in. x 0.38 oz. = 0.21 in.- oz. The rotor velocity coefficient can be calculated from the stall torque with the following equation.

ψR = [(2gTst/(wDciψN) – cosα]/cosβ

ψR = The rotor velocity coefficient
g = The gravitational constant = 32.2 lbm – ft / lbf – sec2
Tst = Stall torque = .21 in-oz x ft/12 in x lbf/16 oz = 0.00109 ft – lbf
w = Mass flow = 1.74 lbm/hr x hr/3600 sec = 0.000483 lbm/sec
D = Rotor diameter = 1.226 in x ft/12 in = 0.102 ft
Ci = Spouting velocity = 1,324 ft/sec
ψN = Nozzle velocity coefficient = 0.96
α = Nozzle angle = 21⁰
β = Blade angle = 25⁰

ψR= [2×32.2x 0.00109/(0.000483 x 0.102 x 1324 x 0.96) – 0.933]/0.906 = 0.21

[Turbine GuyParticipant @turbineguy]

Posted by Jens Eirik Skogstad on 21/12/2019 13:30:27:

Although the horsepower is not high, the horsepower / torque will increase at the reduced speed via the gearbox.See at my steam turbine in this link..

Model steam turbine with 79 mm 4 blade propeller. **LINK**

Model steam turbine with Graupner 65 mm 2 blade propeller (in fault rotation direction) **LINK**

Edited By Jens Eirik Skogstad on 21/12/2019 13:32:01

Hi Jens,

I'm glad to see someone with another turbine. Please tell us more about your turbine and your testing. Any information on model turbines is greatly appreciated.

[Jens Eirik Skogstad 1Participant @jenseirikskogstad1]

Hi Turbine Guy.. see at this link where i wrote about steam turbine. **LINK**

[Turbine GuyParticipant @turbineguy]

Hi Jens Erik,

I followed your link and read all the posts. You and others in this link added a lot of useful information. Thanks for contributing to this thread.

[Turbine GuyParticipant @turbineguy]

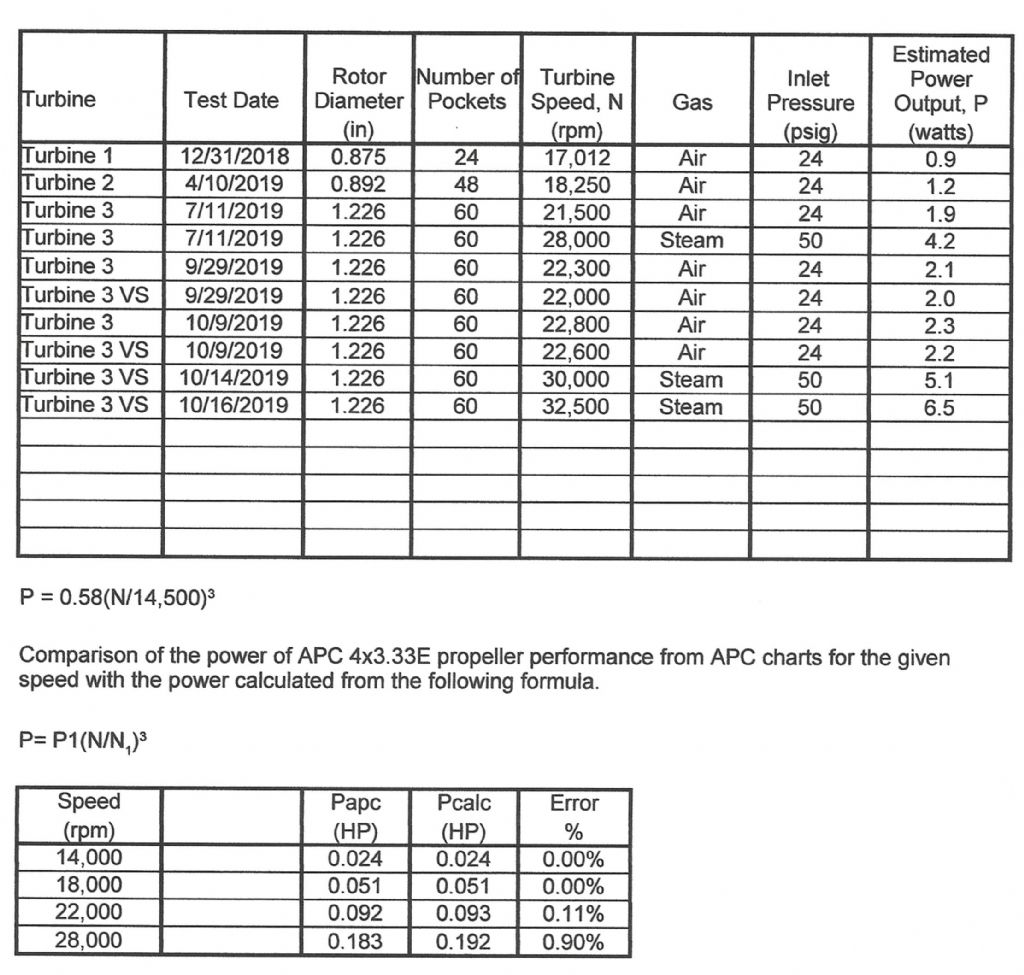
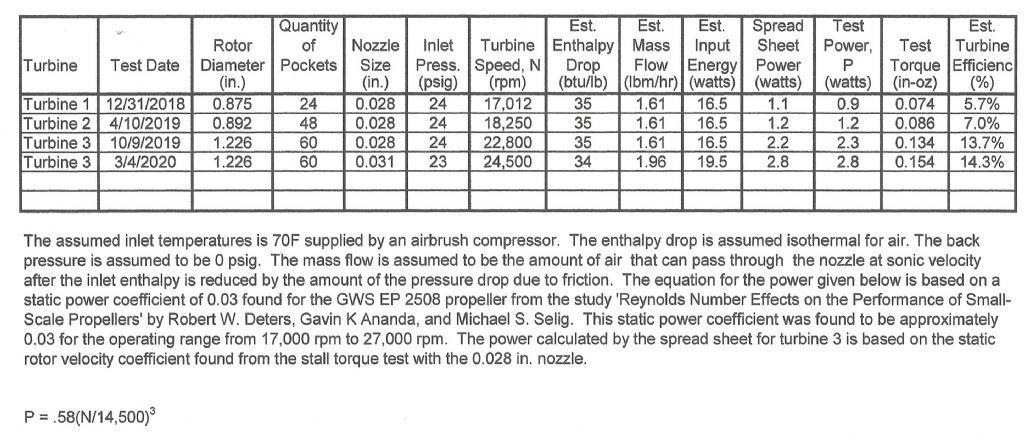
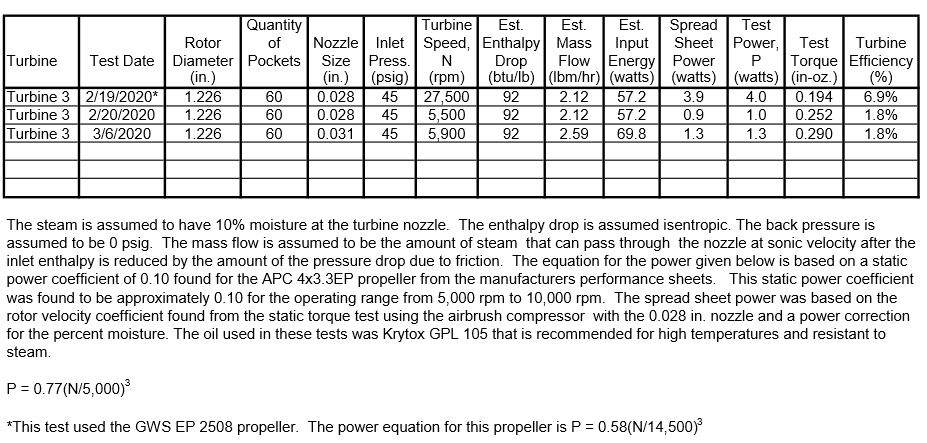
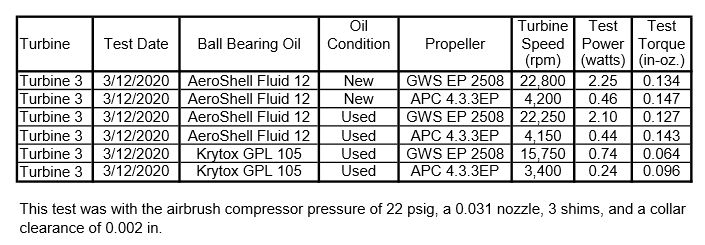
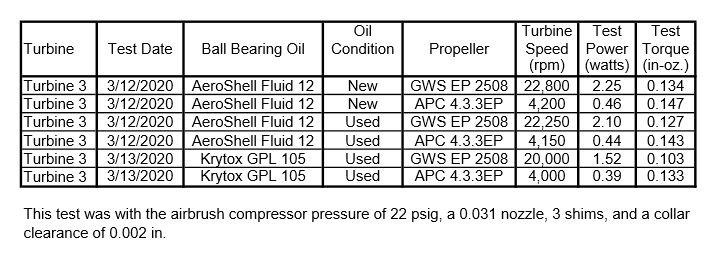
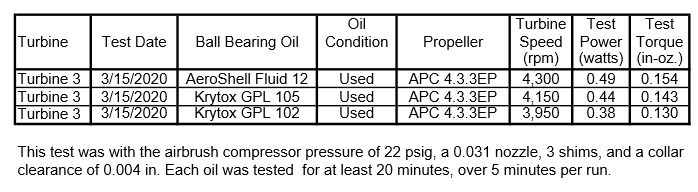
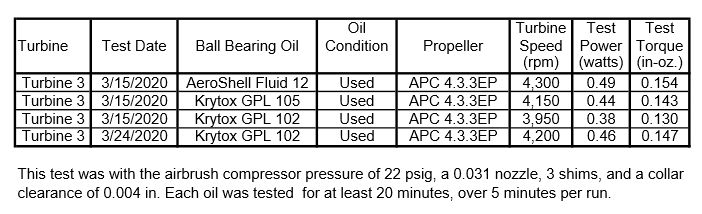
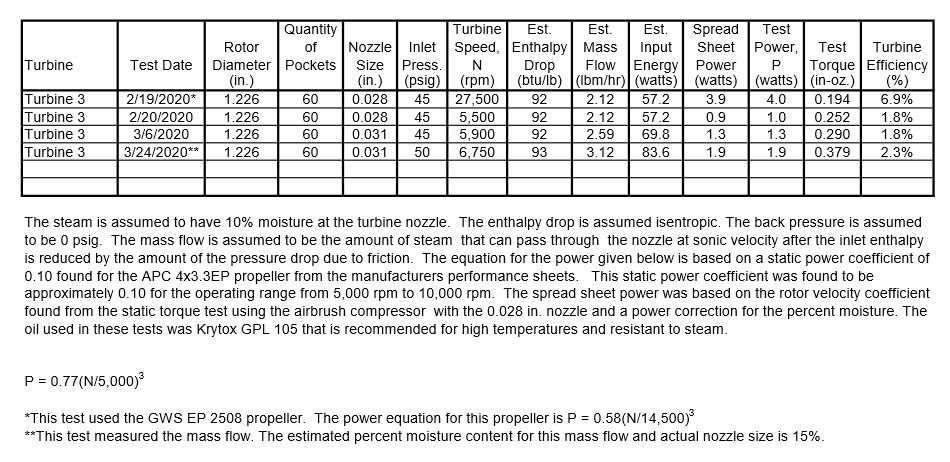
The rotor velocity coefficient of 0.21 found in the post of 21/12/2019 includes all the flow losses including the Reynolds number and empty blade losses. This velocity coefficient can be used to calculate the hydraulic power. The hydraulic torque is the maximum torque that can be obtained for a given rotor tip speed, mass flow, spouting velocity, rotor diameter, nozzle angle, and blade angle without any losses such as friction or windage. All of these parameters except the rotor tip speed were given in the 21/12/2019 post and are shown again below.

ψR = The rotor velocity coefficient
g = The gravitational constant = 32.2 lbm – ft / lbf – sec2
Tst = Stall torque = .21 in-oz x ft/12 in x lbf/16 oz = 0.00109 ft – lbf
w = Mass flow = 1.74 lbm/hr x hr/3600 sec = 0.000483 lbm/sec
D = Rotor diameter = 1.226 in x ft/12 in = 0.102 ft
Ci = Spouting velocity = 1,324 ft/sec
ψN = Nozzle velocity coefficient = 0.96
α = Nozzle angle = 21⁰
β = Blade angle = 25⁰

The equation for the hydraulic torque, Th, is

T_h= wD/2g[ψ_NC_icosα(1+ψ_R) – u(1+ψ_R)]

= 0.000483×0.102/(2×32.2)[0.96x1324x0.933(1+0.21) -u(1+.21)]

= 0.000000765[1435-1.21u) ft-lbf x12in/ft x 16oz/lb

=0.000147(1435-1.21u) in-oz

u= the rotor tip speed, ft/sec

u= πDN/60 = πx0.102xN/60 = 0.00534N

N = Turbine Speed, rpm

Th = 0.000147(1435-1.21×0.00534N) in-oz

Edited By Turbine Guy on 21/12/2019 20:10:07

[Turbine GuyParticipant @turbineguy]

The hydraulic power, Ph, is given by the following equation.

Ph =ThN/63000xlbf/16ozx746watts/HP=0.00074ThN watts

Ph = 0.00074ThN, watts

These are the equations for the hydraulic torque and power for my turbine 3 at the maximum output of my airbrush compressor.  I will add a table showing the values of these at  given turbine speeds and include the values of the power, P, from my turbine 3 spreadsheet that includes friction, windage, sonic losses.

 

Edited By Turbine Guy on 21/12/2019 20:30:51

Edited By Turbine Guy on 21/12/2019 20:36:53

Edited By Turbine Guy on 21/12/2019 21:07:33

[Jens Eirik Skogstad 1Participant @jenseirikskogstad1]

Deleted due double post.

Edited By Jens Eirik Skogstad on 21/12/2019 20:33:31

[Jens Eirik Skogstad 1Participant @jenseirikskogstad1]

Mathematics related to steam turbine is not my strong thing. Only practical experimentation with failure and testing results in the creation of a fully usable steam turbine. With the reduction gear you get better use of steam turbine. Heavy turbine wheels + high revolution above 15 000 rpm = better torque due to stored energy in "flywheel". Small turbine wheel diameter is easy to get high revolution than a large diameter turbine wheel for same steam pressure/velocity.

 

Edited By Jens Eirik Skogstad on 21/12/2019 20:32:33

[Turbine GuyParticipant @turbineguy]

The following data is what I have been trying to post in my last two posts. Copying from a Word file didn't work well because the subscripts were enlarged and the table could not be added. I converted the Word file to a jpeg file and I think this will be easier to read.

Edited By Turbine Guy on 22/12/2019 01:07:10

[Turbine GuyParticipant @turbineguy]

I had a discussion with Mike Tilby about whether the velocity can go supersonic with a converging only nozzle. My sources indicate that the velocity can go supersonic as discussed in the 19/05/2019 post. Because of the large Reynolds number effects of tiny nozzles, I decided to see if this works with miniature nozzles. My estimation for the nozzle maximum velocity running on air at 24 psig, and 1.74 lbm/hr from my airbrush compressor is 1,271 ft/sec. I estimate the sonic velocity to be 1,081 ft/sec. My estimations of the velocities included the pressure loss due to friction in the nozzle. The estimated impact force for these two velocities is 8.7 grams and 7.4 grams respectively. Any reaction force in this range will indicate my estimations are reasonably correct. If the force is above 7.4 grams it will indicate the velocity can go above sonic and will give the approximate amount. If the force is at or below 7.4 grams it will indicate the flow stays at or below sonic. The following photo shows the setup I used to measure the impact force. I supported a cover plate containing the nozzle I estimated the impact forces for in my lathe tailstock. The plate was angled to where the nozzle was perpendicular to the precision scale. As shown in the attached photo the impact force measured was 8.3 grams. This indicated that the velocity may go supersonic in an open space. The remaining question is the effect of the nozzle outlet being so close to the rotor blades or pockets. The pictures and diagrams shown in the post of 29/05/2019 indicate that some distance from the nozzle throat is needed to establish the supersonic velocities. The diverging section of a convergent divergent nozzle allows the gas to reach the maximum velocity before any contact. I doubt that the maximum supersonic velocity can be obtained without some space for the gas to reach full expansion before any contact. For this reason, I tried using the sonic velocity instead of the supersonic velocity in my analysis of the tests for my turbine 3 running on air. This assumes that the loss in velocity is due to the nozzle and the nozzle velocity coefficient is reduced accordingly. When I analyzed the test performance this way, the rotor velocity coefficient increased to approximately the values given in Dr. Balje’s Study of High Energy Level Low Power OutputTurbines.

I forgot when I added this picture that it could not be rotated to the direction the picture was taken. Because of this I normally hold my camera horizontal when taking a photo I want to add to my album. If there is a way to add a photo that has the long dimension vertical into the album correctly or rotate the photo when viewing it, I would greatly appreciate someone telling me how to do it.

[Turbine GuyParticipant @turbineguy]

I weighed the 3/8 oz. jig used to find the stall torque in the post of 21/12/2019 on my precision scale and the actual weight is 0.34 oz. The following sheet shows the update to my estimated performance using this weight and assuming the maximum velocity of the nozzle to be sonic as discussed in the last post. These changes brought the estimated performance very close to that found using the propeller power coefficient described in the post of 7/12/2019. The following is Revision A .

[Turbine GuyParticipant @turbineguy]

The following picture is the one referred to in the last post.

[Turbine GuyParticipant @turbineguy]

In the post of 31/01/2020 I stated that I thought some space was needed from the exit of a converging only nozzle to the first contact with the rotor for the flow to go supersonic. I couldn’t think of a way to provide this space with my tangential rotor, so I tried testing the axial impulse rotors Werner Jeggli sent me. Since the axial nozzle was in a cover plate and the axial rotor could be spaced from the cover plate by shims, I could test the effect of adding space. My testing indicated that the space was important and that the space needs to increase as the Mach number increases. Werner also ran tests that confirmed this. The results of both of our tests indicated that a significant increase in power could be obtained by optimizing this distance. Since my tests were with Werner’s rotors, I’ll leave it to him to provide test results for these rotors. For my tangential rotor, the clearance on the OD of the rotor is important to prevent flow from escaping so I can’t increase this clearance to provide space for expansion. Since running on air from my airbrush compressor results in the ideal flow only going slightly supersonic, I thought I would see the effect of enlarging the nozzle and getting the maximum flow closer to sonic. My calculations indicated that the pressure drop due to friction would decrease because of increased nozzle size and lower velocity. I gradually increased the size of my nozzle about 0.001 in at a time and measured the power. The power increased each time I made an increase in nozzle size. I stopped with the nozzle size of 0.031 in. since there is only 0.002 in. of material remaining on one side with this diameter. I made the following chart to show the significant tests running on air. I only show the maximum power for each of the shown parameters. Some of the results shown in the last chart I provided were caused by changes in friction of bearings after running on steam, a partially plugged nozzle, and changing the minimum thickness of the material around the nozzle. The results of the tests shown in the following chart have values that I get consistently with ball bearings that have only been used with air. I did not include the tests with velocity staging since it was not effective running on air. I will try to do something similar with steam using ball bearings with oil recommended for running on steam at high speeds.

[Turbine GuyParticipant @turbineguy]

The following table is the test results for turbine 3 running on steam. I added the mass flows, input energy, torque, and efficiency for comparison with the test results running on air shown in the last post. I added the torque to the chart because it is much more relevant when I use a larger propeller. The propeller speeds were getting higher than the speeds I could verify the required power of my GWS EP 2508 propeller, so I decided to use an APC 4×3.3 EP propeller for tests with steam. Because the larger propeller requires more torque to turn, the resulting maximum speeds will be much lower and consequently the power and efficiency. With the propellers, the torque is the best measure of performance. For a given energy level, any improvement will increase the stall torque regardless of the size of the propeller. Once the stall torque is determined from testing, the power can be estimated for higher running speeds using the formulas shown on the stall torque test described in the post of 01/02/2020. I tried Krytox GPL 105 oil that Werner Jeggli recommended, and it appears to be working well with my shielded ball bearing. The oil is very viscous when cold but thins out with the steam temperature. I put a small quantity of oil on the outside face of each ball bearing before each test with steam. The oil appears to be getting into the ball bearing through the shields and each run required a short time for the oil to thin out and reach the optimum amount in the bearing. Once the optimum conditions were met, the turbine ran almost constant speed for several minutes. I ran three tests with the 0.031 in. nozzle and the difference in turbines speeds was less than a 100 rpm and the total run time for the three tests was about a half hour. Now that I am getting consistent test results for the 0.031 in nozzle, I will try to come up with a method to measure the mass flow.

[Turbine GuyParticipant @turbineguy]

The following table is a test of the ball bearing oils used in my turbine 3. The ball bearings are supplied with AeroShell Fluid 12 oil. I compared the performance of new bearings with this oil to the performance of bearings with this oil that had been run for quite a while on air and never exposed to steam. I also compared these with ball bearings that had Krytox GPL 105 oil added and had been run on steam for quite a while. Because my turbine 3 is very sensitive to the position of the rotor relative to the nozzle, I ran all these tests with 3 shims and a clearance between the set screw collar and the bearing of 0.002 in. This ensured that the position of the rotor relative to the nozzle was within 0.002 in. for each of the tests. This is not the optimum position for both propellers, so the powers achieved in this test are not as high as I have obtained running on air. The loss in power with the Krytox GPL 105 oil is due to very high viscosity at room temperature that is approximately 14 times as much as the AeroShell Fluid 12 oil at room temperature.

[Turbine GuyParticipant @turbineguy]

The low power for the tests with Krytox GPL 105 oil in the ball bearings shown in the last post seemed lower than expected. I ran several more tests with the Krytox GPL 105 oil and each of my propellers. I found that if the turbine was run for several minutes the speed would go up in small jumps as the thick oil thinned out and got pushed into the optimum position. The first test with each propeller took the longest to obtain the maximum speed. Each later test took progressively shorter time to reach maximum speed. Once the maximum speed was reached, the speed would stay approximately the same for the rest of the time of the test. I repeated the tests several times and each time, the maximum speed stayed approximately the same. The following chart is updated to show the results of these tests and is more like what I expected.

[Turbine GuyParticipant @turbineguy]

I tried to find a source where I could purchase AeroShell Fluid 12 oil. The only sources I found sold the oil in gallons and consequently was VERY expensive and much more than I would ever need. I looked at similar oils and the most promising oil available in small quantities was Krytox GLC 102 which could be purchased from Amazon at a cost of about $35 for 1 oz. This is the same as what 1 oz. of Krytox GLC 105 costs. The two oils are similar, and the biggest differences are low temperature viscosity and temperature limit. The properties are shown in the following table provided by Chemours. I will replace the factory oil in my older ball bearings with the Krytox GLC 102 and see how it compares with the factory oil. If it works as well as AeroShell Fluid 12, it will allow me to periodically add oil as needed. I still plan to use the Krytox GLC 105 when I run with steam since it appears to be working well. Both oils are very expensive, so hopefully they will last a long time. If I only ran my turbine a few minutes at a time periodically on air, I would probably never need to add oil.

[Turbine GuyParticipant @turbineguy]

I decided to test the three different oils discussed in the last post for a running time long enough to see how their performance holds up. I decided that a total run time of over 20 minutes would give an indication of their live expectency and consistency. I also decided to run all the tests with the APC 4×3.3 EP propeller since it is what I plan to use for future testing. I made one short run with the GWS EP2508 propeller with the AeroShell Fluid 12 oil at the end of the tests with this oil. The maximum speed reached was 24,500 rpm, the highest speed I have been able to obtain with this propeller running on air. This showed the maximum power was still the same after running quite a while with this oil. The maximum speeds for the APC 4×3.3 EP propeller for all the oils were at least as high as when the oil was new. The following table gives the results of these tests. The Krytox GLC 102 oil did not perform as well as I hoped. I don’t know if this is because of the way I added it or if the oil is not as suitable for my application. I can’t remove the shields from the bearings I use, so I tried removing the existing oil by soaking the bearings in Acetone and then adding the new oil by letting it seep into the bearings through the small gap in the shields. I don’t know how effective that was in removing the old oil or adding the new oil. When I added the Krytox GLC 105 oil I didn’t do anything to remove the existing oil and just relied on the steam to flush it out or the existing oil to be compatible. I applied a small amount of Krytox GLC 105 to the faces of the ball bearings before each run with steam which appeared to work for adding this oil. Even with the much higher viscosity at low temperatures, the Krytox GLC 105, worked better than the Krytox GLC 102 running with air. Based on these tests, I believe the ball bearing as supplied with the AeroShell Fluid 12 will work fine and have adequate life when running on air. The Krytox GLC 105 appears to work well with steam and results in only a small loss in power running on air. I will use the ball bearings with the Krytox GLC 105 for all my tests that don’t require the maximum power running on air.

[Turbine GuyParticipant @turbineguy]

Since my turbine 3 has multiple openings required for the different options, I can’t channel all the steam into an exhaust tube and measure the mass flow by cooling and collecting the exhaust. I thought I would try making a second nozzle as shown in the following drawing. This would increase the flow and drop the pressure in my boiler below the pressure the relief valve opened. All the mass flow out of the boiler would then go through the turbine nozzles. With the wick type of burner I use, I can run the boiler until it is empty before pulling out the burners. I can then fill the boiler with a measured amount of water and make my test run the amount of time to boil out all the water. This was the plan, unfortunately even with my very careful setup the drill drifted out of position and the second nozzle could not be used. Fortunately, I am still able to use the existing nozzle. I ran a test with steam to check if there was any damage to the existing nozzle and the maximum speed stayed at almost a constant 6,150 rpm for the approximately 7 minutes of the test. This is slightly higher than the maximum speed of 5,900 rpm I was able to obtain in prior tests with steam at approximately 45 psig, with the APC 4×3.3 EP propeller, and using Krytox GLC 105 oil. More of this oil was able to get inside the shielded ball bearings since the speed running on air after the test with steam was lower than before the test with steam. I am expecting the speed to gradually increase when running on air after the oil wears and thins out like it has after prior tests with steam.

[Turbine GuyParticipant @turbineguy]

The safety valve on my Stuart Turner 504 boiler that was purchased in the 1970’s was releasing steam at a pressure of around 45 psig (3 bar). The maximum operating pressure for this boiler is given as 60 psig (4 bar). I don’t have a way to measure the size of the threads on the safety valve, so I searched the internet. In this search, I stumbled on the video shown in this this link https://www.youtube.com/watch?v=O05uMDICFWk. The video gave the thread size but also gave suggestions for repairing the safety valve. I tried adding a washer and sealant as suggested in the video and checked the release point with these changes. The release point was slightly over 60 psig and almost all the leakage from the valve was stopped. I ran the boiler dry and then added a carefully measured ¾ cup of water. I then ran the boiler with my turbine 3, APC 4×3.3EP propeller, and Krytox GLC 102 oil. After a short time, a turbine speed of 6,800 rpm was reached and held approximately constant for the rest of the run. The total run time was 7.5 minutes. I wanted to learn two things from this test, the mass flow out of the boiler into the turbine and if the Krytox GLC 102 oil worked better after running on steam. Since there was no release or leakage from the safety valve, all the flow went to the turbine and the pressure reached 50 psig (3.5 bar) with the 0.031 in. nozzle. The mass flow was approximately 3.1 lb/hr (23 g/min). After running on steam, the maximum speed running on air was 4,200 rpm so the performance of the Krytox GLC 102 did improve as shown in the following table. Apparently the high temperature of the steam thins the oil enough that it can expel the excess and obtain the optimum amount.

Edited By Turbine Guy on 25/03/2020 16:43:47

[Turbine GuyParticipant @turbineguy]

I updated the turbine test results for running on steam as shown in the table below. As described in the last post, fixing the safety valve on my boiler stopped the leakage and allowed the pressure to get high enough that all the flow went to the turbine. This allowed me to measure the mass flow and estimate the actual percent moisture. The estimated 15% moisture found in this test was higher than the 10% I had been assuming.

[Werner JeggliParticipant @wernerjeggli14222]

Hello Byron,

I do not understand why the turbine is running at such a low speed. With steam and at this pressure, this should be in the vicinity of 30'000 rpm. The torque will stay approx. the same, but the power output will rise proportionally.

[Author]

Posts