Fedchenko isochronous suspension

[david bennett 8Participant @davidbennett8]

Has anyone made a working reproduction of Fedchenko's isochronous suspension/pendulum ?

dave.

Edited By david bennett 8 on 17/02/2023 06:14:32

[david bennett 8Participant @davidbennett8]

[Clive SteerParticipant @clivesteer55943]

Although Fedchenko described his suspension there were no construction information or dimensions so replicating it would require a degree of experimentation . However he explains in his article a couple of other methods that, although not as effective as his design, could reduce the effects of circular error. The two that are relatively easy to construct area the cycloidal cheeks acting on the suspension spring and an extension coil spring acting on the pendulum rod to provide extra restoring force proportional to pendulum amplitude.

Cycloidal cheeks may only be effective for larger amplitudes as dimensional accuracy and suspension spring compliance may make things difficult. I think it may be possible to simplify the cheeks by using pins and if adjustable could be tweaked to get thee required result.

The spring method was used, very successfully on Bulle electric clocks to stabilise pendulum amplitude with variations in battery voltage and used a simple single rate extension coil spring. However the use of multi-rate spring may give better results.

Testing for an isochronous pendulum is quite simple in that one pulls the pendulum to one side and let it go and then log the timing as the amplitude decays.

CS

[BazyleParticipant @bazyle]

The manufacture of cycloidal cheeks sounds like a job for modern computers to design and CNC or even 3D printing to produce. perhaps more effective on 'simple' clocks with high amplitude swings like cuckoos etc.

[John HaineParticipant @johnhaine32865]

All real pendulums are compound as their mass isn't focused at a single point. It has been proved that there is no cheek profile that can make a compound pendulum isochronous. A circular profile as used in Clock B can probably compensate over a limited amplitude range provided the spring only starts to wrap beyond a certain threshold. I think it was Peter Hastings who published the use of a pin (or pins?) in HJ and they could be as good as circular cheeks and much easier to make!

I had a go at making circular cheeks by CNC though I didn't test the result. It would be easy to make cycloidal cheeks – just different equations to generate coordinates – though a bit pointless.

Though I don't think anyone has made Fedchenko springs Philip Woodward analysed them – I'll look up the reference.

Done – HJ March 99 pp82-84.  It includes some references to HSN and elsewhere that have further information.

Edited By John Haine on 17/02/2023 11:15:58

[Martin KyteParticipant @martinkyte99762]

Just read Fedchenko’s paper which was fascinating.
I have never heard of a precision timekeeper employing a balance wheel which suggests there are some inherent problems which limit their performance. Anyone care to comment? I’m not talking about chronometers but something on a par with the best pendulum timekeepers.

regards Martin

[Peter Cook 6Participant @petercook6]

Posted by Martin Kyte on 17/02/2023 11:46:01:

I have never heard of a precision timekeeper employing a balance wheel which suggests there are some inherent problems which limit their performance. Anyone care to comment?

I would imagine the issue is a basic problem with using a spring as the restoring force as the oscillator swings.

Gravity is pretty consistent (in the short term) as a restoring force acting on a pendulum, and the same in both directions of the swing.

A balance wheel obtains its restoring force from the balance spring and as a minimum – and probably inherently – the force in the two directions, one as the spring coils up from the mean position and one as the spring uncoils from the same position, will be different.

Gravity is a lot easier to get consistent.

Edited By Peter Cook 6 on 17/02/2023 12:09:02

[Michael GilliganParticipant @michaelgilligan61133]

I posted this on another thread recently … but it it might be convenient to also have it here

____________

Fedchenko’s rather special pendulum suspension spring is described: **LINK**

https://articles.adsabs.harvard.edu/pdf/1957SvA…..1..637F

___________

MichaelG.

[david bennett 8Participant @davidbennett8]

I was viewing the spring/s as only coming into play to prevent overswing of the pendulm /suspension – one on either side of the pendulum, each the opposite way round.

dave.

,

Edited By david bennett 8 on 17/02/2023 16:37:56

Edited By david bennett 8 on 17/02/2023 16:51:51

[Martin KyteParticipant @martinkyte99762]

Posted by Peter Cook 6 on 17/02/2023 12:07:56:

Posted by Martin Kyte on 17/02/2023 11:46:01:

I have never heard of a precision timekeeper employing a balance wheel which suggests there are some inherent problems which limit their performance. Anyone care to comment?

I would imagine the issue is a basic problem with using a spring as the restoring force as the oscillator swings.

Gravity is pretty consistent (in the short term) as a restoring force acting on a pendulum, and the same in both directions of the swing.

A balance wheel obtains its restoring force from the balance spring and as a minimum – and probably inherently – the force in the two directions, one as the spring coils up from the mean position and one as the spring uncoils from the same position, will be different.

Gravity is a lot easier to get consistent.

Edited By Peter Cook 6 on 17/02/2023 12:09:02

And yet balance wheels can be adjusted to be Isochronism and temperature compensated and do not have a buoyancy problem. They move faster so drag could be an issue. There must be some basic brick wall or the things would exist?

regards Martin

[duncan webster 1Participant @duncanwebster1]

Marine chronometers have balance weights, and they are pretty good, not in Fedchenko league. Balance wheel has to have bearings, so energy loss. Difficult to make high Q?

Edited By duncan webster on 17/02/2023 17:26:23

[Martin KyteParticipant @martinkyte99762]

The best Q I could find doing a quick google was 650 but more typically between 200 and 300 but that that is for watches, without the space constraint I’m sure that could be improved on but as you say it’s several orders of magnitude lower than a good pendulum.

regards Martin

PS anyone know what the Q of H3’s balance wheels was.

Edited By Martin Kyte on 17/02/2023 17:49:36

[david bennett 8Participant @davidbennett8]

I was looking at Fedchenko's suspension springs, unusual in that they make two outward curves at each end to meet the thicker sections. I wonered if they made a difference to the circular error, as the top of the spring would flex more than the bottom. This led me to wonder if a spring made to some specific curve to the thickness of the spring (difficult ) or the width (easy ) could be isochronous. As I have no timing equipment nor do I understand it, I was hoping someone cold do a quick and dirty comparison between a piece of raw suspension spring and then roughly shaped to an involute (?) curve. Or am I just being naive over the whole subject?

dave8

Edited By david bennett 8 on 20/02/2023 21:01:14

Edited By david bennett 8 on 20/02/2023 21:06:21

Edited By david bennett 8 on 20/02/2023 21:15:43

[John HaineParticipant @johnhaine32865]

Various people have analysed suspension springs to see if a single spring can counteract circular deviation – names to look for are Kenneth James and Philip Woodward. But the answer is no, except for Fedchenko which is a compound spring.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by david bennett 8 on 20/02/2023 21:00:09:

I was looking at Fedchenko's suspension springs

[…]

Or am I just being naive over the whole subject?

dave8

.

Slightly confused here, Dave [please forgive me if I have missed the point]

… You do not appear to be considering what is described around Fig.4 in Fedchenko’s paper that I linked.

MichaelG.

[david bennett 8Participant @davidbennett8]

Michael, yes he says "misunderstanding", but I still don't know what it is. So "naive" it is. Thanks all for saving me some time over this.

dave8

Edited By david bennett 8 on 20/02/2023 22:08:33

[Michael GilliganParticipant @michaelgilligan61133]

This will probably sound glib, Dave … but that’s because I don’t understand sufficiently well to give a complicated answer !!

I think what he’s really saying is that problem is too complex to be solved by cleverly shaping a spring … it demands the dynamic interaction of three springs to achieve the necessary motion.

MichaelG.

[david bennett 8Participant @davidbennett8]

Michael, thanks for trying to clarify! While I have the greatest respect for any expert in their field, I have to retain my right to be a "doubting Thomas" until I prove it for myself (though not in this case) I have known too many cases where conventional wisdom has proved wrong.

Dave8

[John HaineParticipant @johnhaine32865]

The reason they curve from the thinner to the thicker sections is because they are machined out of the thicker base material. If the transition was square it would probably quickly fracture. Matthys describes making springs from phosphor bronze strip by milling both sides of the spring section away with the side of an end mill, the material being clamped flat on a vertical face. Having machined one side it was turned over and re-clamped with the space filled with plaster of Paris for support. Tricky! But that obviously leaves the curved transition.

[Michael GilliganParticipant @michaelgilligan61133]

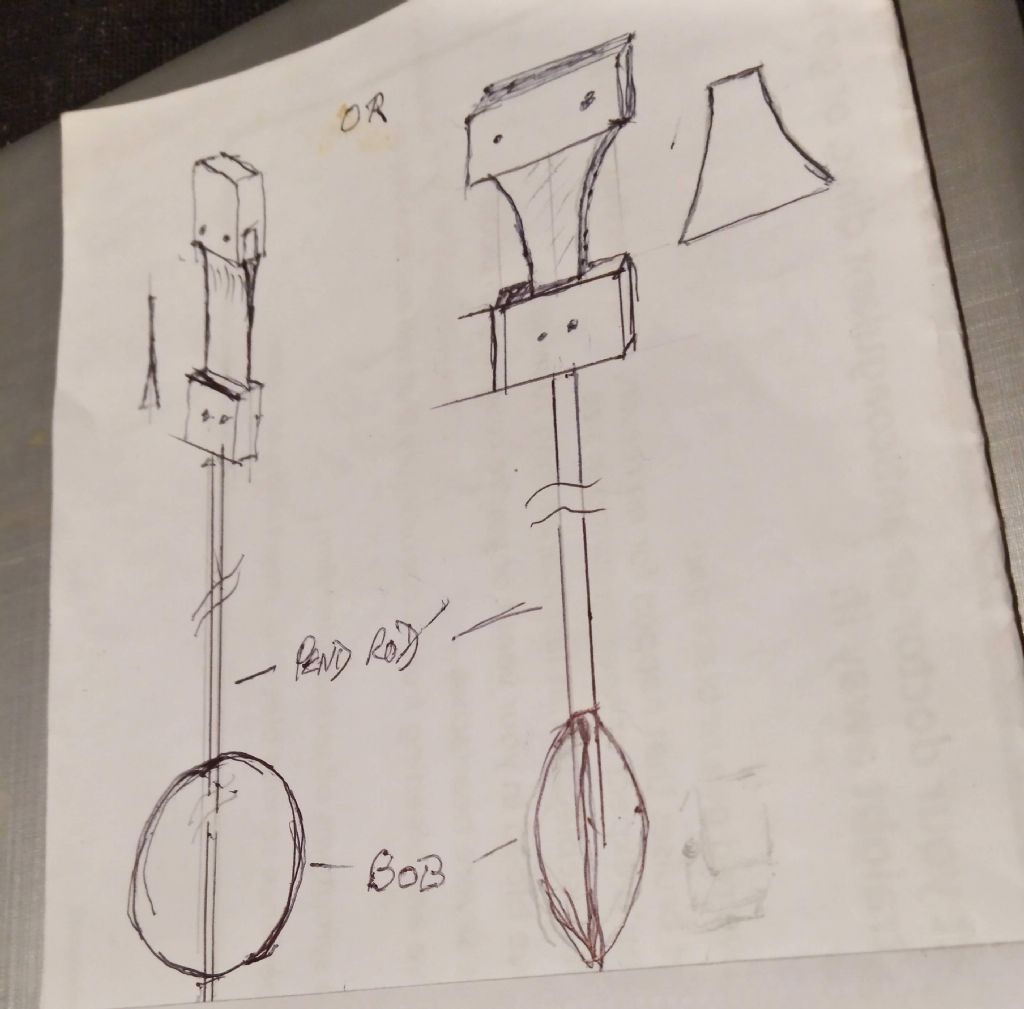
Posted by david bennett 8 on 21/02/2023 00:30:10:

[…]

I have to retain my right to be a "doubting Thomas" until I prove it for myself (though not in this case) I have known too many cases where conventional wisdom has proved wrong.

Dave8

.

Good Man

I fully support your right to that.

MichaelG.

.

Edit: 

Towards the top of p.640 Fedchenko states:

Numerous experiments conducted with various suspensions have confirmed that isochronism of oscillations of a free pendulum  cannot be attained by altering either the dimensions or the shape of the springs of the suspension.

.

Note: __ I have intentionally kept the double space before the word cannot … because we might conceivably see that as a sign of hesitation, or of editorial input:

Use of the word is not scientifically appropriate!

Did he really mean “are very unlikely to”

We shall probably  never know … but it’s a straw to grasp.

Edited By Michael Gilligan on 21/02/2023 08:33:59

[John HaineParticipant @johnhaine32865]

It's not as if people haven't investigated this before – I mentioned Kenneth James before, and Philip Woodward. Fedchenko points out that the restoring force from a straight spring has the wrong power law, being linear with deflection angle whereas the required force needs to have a cube law term. A double space is more likely to be a publication artefact bearing in mind that the paper dates from 1957 and could well be a translation from Russian.

Now I'm wondering if I should try to make a Fedchenko suspension?

[Michael GilliganParticipant @michaelgilligan61133]

Posted by John Haine on 21/02/2023 09:44:50:

[…]

A double space is more likely to be a publication artefact bearing in mind that the paper dates from 1957 and could well be a translation from Russian.

.

I know, John … but I was merely providing alternative explanations for the inclusion of a statement that is scientifically unacceptable.

Absence of proof is not proof of absence. … and “numerous experiments” are not sufficient to confirm that something cannot be done.

MichaelG.

[Clive SteerParticipant @clivesteer55943]

It isn't clear to me whether the Fedchenko suspension arrangement provides the desired cube law restoring force or made the pendulum bob track a cycloidal path.

Frodshams have lent me the "Harrison Decoded" and the "Woodward on Time" books to bring me up to speed on Pendulums.

One point made in the Harrison Decoded book is the importance of "The Hill test" . It seems the cycloidal cheeks are profiled to not only reduce circular error but to overcompensate for this at the proposed working pendulum amplitude. Beyond this amplitude the timing increases and below this amplitude follows a reduced circular error profile. I still need to understand precisely how this is used to balance the effects of buoyancy and aerodynamic drag.

CS

[Martin KyteParticipant @martinkyte99762]

Posted by Michael Gilligan on 21/02/2023 09:56:05:

Posted by John Haine on 21/02/2023 09:44:50:

[…]

A double space is more likely to be a publication artefact bearing in mind that the paper dates from 1957 and could well be a translation from Russian.

.

I know, John … but I was merely providing alternative explanations for the inclusion of a statement that is scientifically unacceptable.

Not sure that using confirmed is scientifically unacceptable. Proved maybe but usually confirmed means in agreement with other results and conclusions.

Absence of proof is not proof of absence. … and “numerous experiments” are not sufficient to confirm that something cannot be done.

I think you have to be a little careful in using that statement. It holds better in situations where different events are equally likely to occur and are physically possible but expecting a spring to deviate from a linear law to a cubed law sits on 300 years of experimental evidence so practically speaking is as close to proof as you get. In one sense you are right though there are no absolute proofs in science only disproofs.

.MichaelG

Regards Martin

PS My bits in bold

Edited By Martin Kyte on 21/02/2023 10:55:47

[John HaineParticipant @johnhaine32865]

Clive, over on another thread I posted this link: **LINK**

which is the analysis that Andrew Millington and I did of the system. In our view it's quite a lot easier than "Harrison Decoded" implies. In order to get a "hill" you need to nearly but not quite compensate for circular deviation around the running amplitude. One thing we pointed out is that it relies on quite a high escapement deviation as part of the "balance", which means you need a large impulse and that means a lowish Q to control the amplitude. Something I've realised since is that the system relies on the amplitude responding quite quickly to pressure variation if you are going to cancel out the buoyancy change in rate, another reason for a lower Q.

If you have WOT the chapter on Fedchenko starts on p243 – the references are well worth finding as well.

[Author]

Posts