Posted by duncan webster on 10/12/2022 23:59:11:
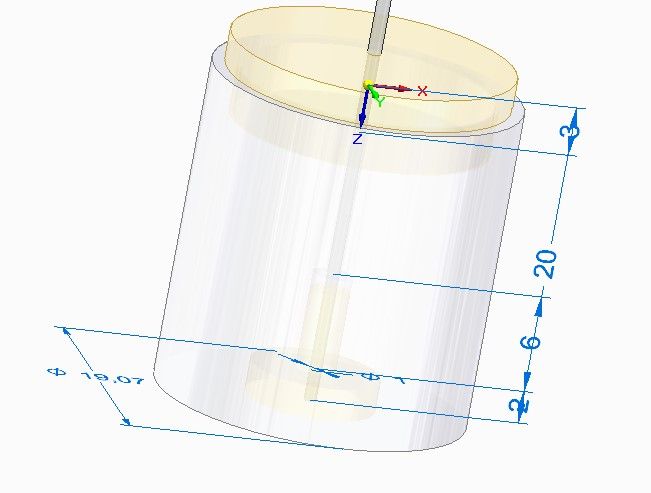
I wouldn't jump ahead too far. I imagined the ally going between the end stop on the cf and the seating halfway up the bob. Actually just above half way as the hole in the bottom bit is bigger than the hole in the top bit so the cg is just over half way up. Not by much tho as the holes are small compared to the OD. Then the whole bob is lifted up. However, with it suspended as you have it from the bottom, the bob expands upwards relative to the end stop, and I'd expect that to be more than the expansion of the suspension spring. So I'm a bit unsure of what's going on. I'd start by moving the suspension point to the cg, get rid of the top brass disc ( I have a split lightweight collet) and then establish the time/temperature relationship. In an ideal world you'd do this by enclosing it in a controlled temperature environment, you might be able to extract it from all the other variables using statistics. Then fit an appropriate washer, which can be C shaped so it can just be slipped on after lifting the pendulum.
Agreed! I like the collet idea.
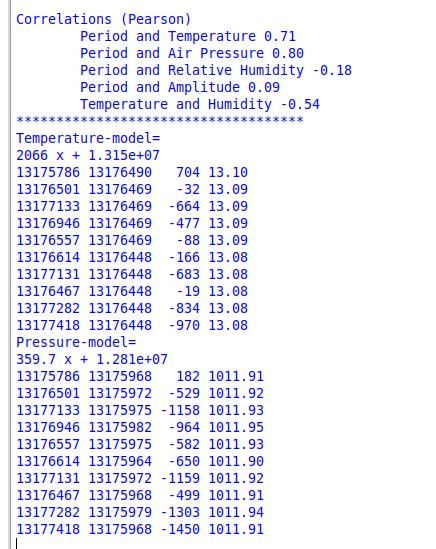
On Friday I added the code needed to extract the correlations, with these results:

Spent yesterday in a muddle about how to apply the information. Pearson shows strongish positive correlations between period (ticks) and temperature and period and pressure. There's also a correlation between temperature and humidity, but I don't think it matters.
My first problem is how to combine two formula!
tick = 2066 * temperature + 1.315e+07 AND tick = 359.7 * pressure + 1.281e+07
My brain has seized. I've failed to define f(temp, pressure) giving tick.
Second problem is, having predicted what the correct tick should be by applying temperature and pressure, what maths is needed in the motion to apply the information. (The period was 'n', due to known temp and pressure, what should period be changed to before input to the counter.)
Yesterday morning I thought both questions were easy. Perhaps they are, but I'm baffled!
Dave
Edited By SillyOldDuffer on 11/12/2022 11:52:48
duncan webster 1.