Posted by SillyOldDuffer on 21/02/2023 08:56:49:
Posted by John Haine on 21/02/2023 07:21:33:…
then supposing a clock that started at zero in the period just before e1, form the sequence:
0, 0+e1, 0+e2+e2, 0+e1+e2+e3, ….
where each term is the previous one plus the new error. This sequence would be the time, or phase, error of the clock from perfect time. This is the sequence to compute ADEV from.
…
Excellent thanks, I understand!
A rolling sum exactly as you said in the first place, sorry it didn't click. Off to try it now.
Ta,
Dave
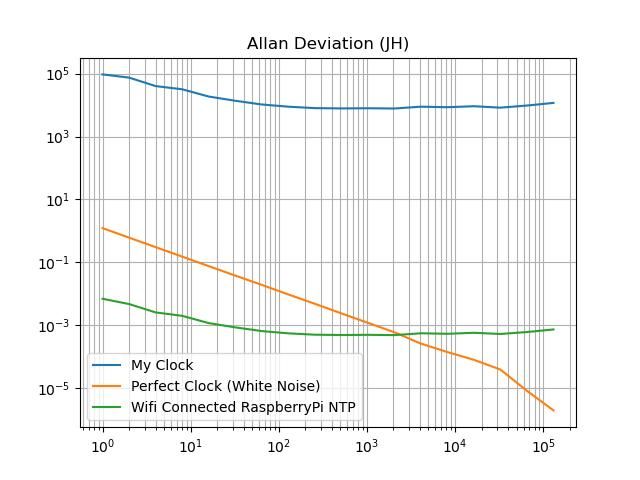
Would have reported earlier except I added a 'perfect clock' and 'Raspberry Pi NTP' for comparison:

Interpreting this, I offer:
- The direction of slope is as important as position on the Y-scale (Allan Deviations), but
- good clocks have lower Allan Deviation values than bad ones, also
- The X-Scale (measurement intervals, taus), should be read left to right in 5 sectors:
- White Phase Noise (unavoidable in any system)
- Phase Flicker Noise
- White Frequency Noise
- Frequency Flicker Noise (mechanical issues)
- Random Walk Noise (caused by an environmental change triggering a temporary variation in rate)
My feeling is noise is only significant in really good clocks, that is the graph helps diagnose problems once a clock has been thoroughly debugged. Gross errors, like the suspension working loose, don't need Allan Variance to diagnose the fault. I think Allan is useful when there's a desire to improve an already good clock.
So, not unexpectedly my clock is well up the deviation scale (lots of noise), and the flat line line indicates that the main problem is Frequency Modulated Flicker, where the clock's rate is constantly disturbed.
The 'Perfect Clock' is represented by White Noise, in which there is no Flicker or Random Walk noise. It's slope marches down at about -0.5.
The Green line is NTP as measured by my clock ticking a raspberryPi (which adds NTP timestamps). So the slope of the NTP line is dominated by my clock's Frequency Modulated flicker, but the superior stability of NTP shows up by the line being much lower down the Y-scale.
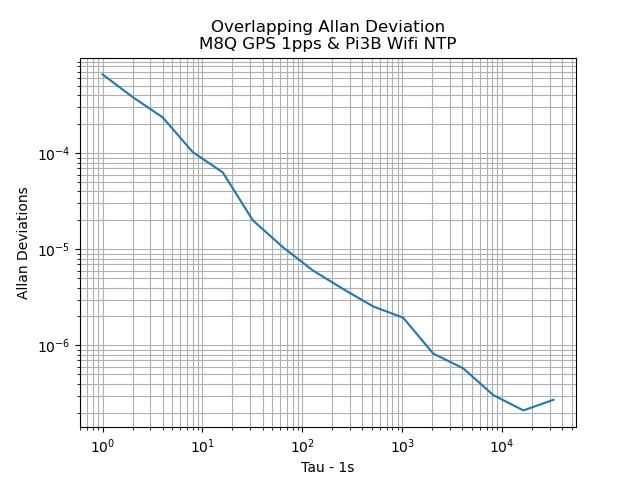
GPS seconds are the closest I can get to a perfect clock, so I'll try NTP timestamping it's output, and running Allan on the result. I think that will give a reasonable measure of the Allan Variance of NTP on my raspberryPi. The variance should be low, but far from perfect.
Won't take long but I have to out. A job for this evening.
Does my explanation of Allan sound reasonable? I believe I'm gradually making sense of Rawlings, Chapter 18, but could be wrong.
Dave
duncan webster 1.


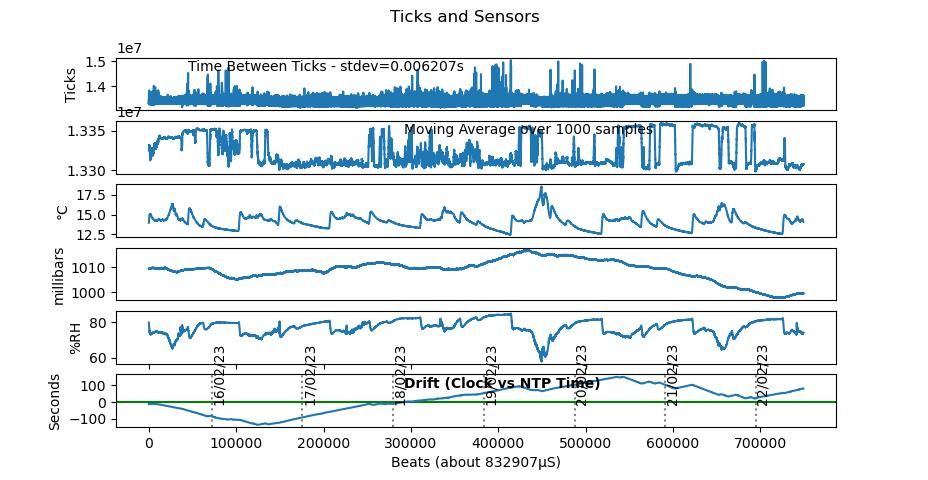
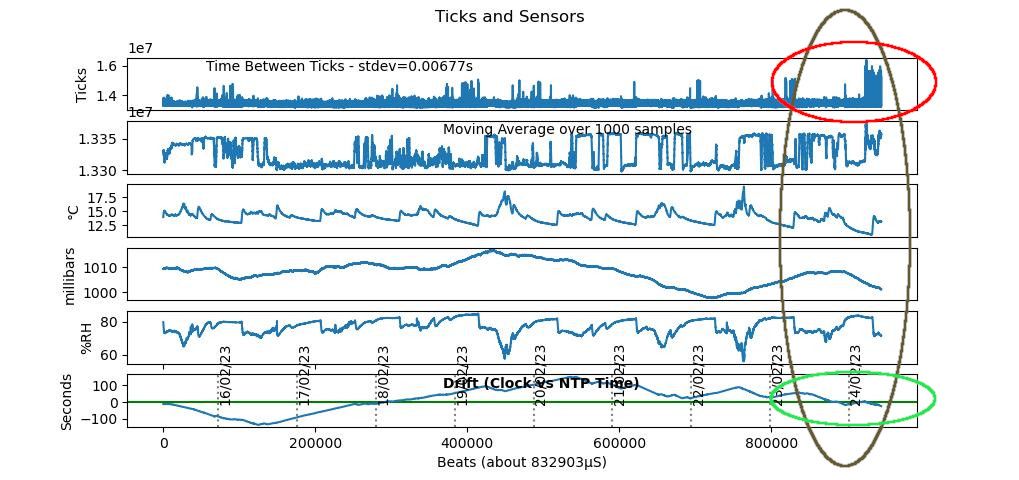
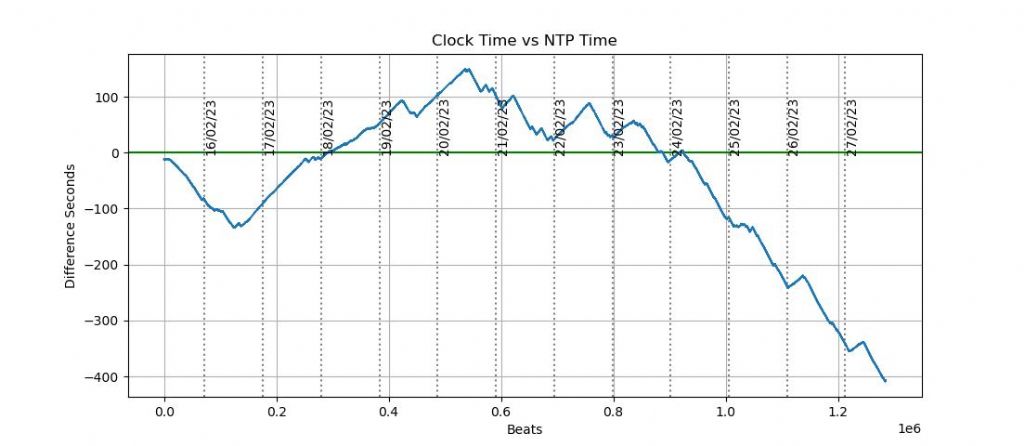
 . It's done particularly well over the last 14 hours, where it's kept good time (green ellipse). And overall, there's comfort in the whole trace not veering to one side of the line: on average it's not fast or slow.
. It's done particularly well over the last 14 hours, where it's kept good time (green ellipse). And overall, there's comfort in the whole trace not veering to one side of the line: on average it's not fast or slow.