Experimental Pendulum Clock

[SillyOldDufferModerator @sillyoldduffer]

Ages ago I built a pendulum clock with a bob on the end of a short thin carbon rod with no suspension, the idea being that the rod would act as a spring that's not temperature sensitive. Didn't keep good time, partly because the rod tends to swing in an ellipse, with low Q, and partly because it's sensitive to humidity. (I guess the plastic matrix is effected and humidity alters it's springiness, nothing to do with the fibre.)

Bit of reinventing the wheel because I can't find the notes describing where I'd got to, but I've made a start by adding a suspension:

Zooming in on the suspension, I'd welcome comments on the design:

The spring, 0.1mm thick, is cut from the blade of a disposable razor, edge blunted to avoid spilling blood. It's clamped between brass cheeks, with about 2mm free to flex. The 0.8mm diameter carbon fibre rod is superglued into the cone, which is 10mm long. Is this a good design?

The results are odd. The graph is a run of about 25 hours,

The top graph shows tick times vary and that the variation is slowly getting worse. A perfect pendulum would graph as a straight line. Worse than expected; the average tick is 13369412 Arduino Clock Cycles, which has a 16MHz quartz crystal, actually averaging 15998101Hz. However the fastest tick took 13275269 cycles, and the slowest 13471208. The range is 195939 cycles, about 0.012s, which I feel is too much.

The second graph is a moving average of the first. It shows that the pendulum is gradually speeding up, and its not related to temperature, air pressure or humidity.

Most confusing is the third graph, which is the wrong shape! It counts the number of beats in each of 20 buckets across the range of variation and shows the slow and fast tick counts, both outnumber the average. I'd expect the distribution to be concentrated in buckets closest to the average. Instead, the graph implies the pendulum has two modes of oscillation.

Any ideas what might cause a pendulum to display these symptoms?

Dave

[SillyOldDufferModerator @sillyoldduffer]

[Anonymous]

How do you know that the Arduino Clock Cycle is accurate and stable? A quartz crystal probably won't vary enough to give the results seen. But they do drift, usually 50 to 100ppm at the lower cost end. Stability is also dependent on the quality of the oscillator. Presumably there is softare between the crystal oscillator and the measurement being made?

Andrew

[Robert Atkinson 2Participant @robertatkinson2]

Apart from Andrews comments re the reference, if this is the first period of running, could it be due to changes in the flexture? Either work hardening or fatigue. I guess use as a pendulum flexture was not on the razor designers mind when the chose the steel for the blade.

On references, how do you know the Arduino crystal is 15.998101 MHz? The crystals used for microcotrollers are not known for their accuracy.
Confession, I'm a bit of a electronics "time nut" with 6 GPS disciplined oscilators / clocks, half a dozen Rubdium atomic oscillators, several high performance crystal ocillators, counters to 20 picosecond resolution and frequency difference measurement to better than 1 part in 100,000,000,000. I normally have 3 references running.

Robert G8RPI.

[Michael GilliganParticipant @michaelgilligan61133]

Instinct says that your spring is too short an too thick, Dave

… I think that you might find the rod is taking some of the bending.

As a quick check … try clamping a few strands of silk thread [or some-such] between the cheeks instead of the razor blade.

MichaelG.

[duncan webster 1Participant @duncanwebster1]

Many moons ago, razor blades were the go to source for suspension springs for home made clocks. These would have been the old carbon steel ones. I used some 0.004" stuff I got from who knows where. Not stainless but too hard to drill, had to punch it. Humidity has 2 effects apart from any material effects, firstly it makes the air less dense, so it reduces buoyancy, effectively increasing g. Second less dense air will have lower drag. I was advised by a BHI chap to make my suspension spring 'no more than 10 mm'. I know 2mm is not more than 10, but it's at the other end of the spectrum. All depends on angle of swing I suppose. How constant is that?

Edited By duncan webster on 28/11/2022 00:36:22

[John HaineParticipant @johnhaine32865]

Does your illustration show the full cheek arrangement or is it missing the clamping part?

[SillyOldDufferModerator @sillyoldduffer]

Posted by John Haine on 28/11/2022 08:10:14:

Does your illustration show the full cheek arrangement or is it missing the clamping part?

Easy question first: to show the construction I left the clamps out of the illustration. In complete form it looks like this:

The clamps are threaded M2, and each is pulled against the body by single M2 screw passing through the square holes fortuitously added to the razor blade by the manufacturer.

A few more construction details, because the whole thing is novel. The free-standing clock is less than 300mm high and the pendulum frame is a tripod made of aluminium tubing braced by M4 studding. I assume it's proportionally rigid compared to the small bob:

The structure is sized to fit inside a length of drainpipe and evacuated so the bob swings in a good vacuum. The feature is built but not tested because the pendulums performance so far isn't good enough to justify pumping the air out.

And a shot of the actual suspension:

Dave

Edit Ooops.  Fixed the photos, thanks Michael!

Edited By SillyOldDuffer on 28/11/2022 10:09:11

[Michael GilliganParticipant @michaelgilligan61133]

You need a Moderator to rotate those photos, Dave

MichaelG.

[SillyOldDufferModerator @sillyoldduffer]

Posted by Michael Gilligan on 27/11/2022 21:46:14:

Instinct says that your spring is too short an too thick, Dave

… I think that you might find the rod is taking some of the bending.

As a quick check … try clamping a few strands of silk thread [or some-such] between the cheeks instead of the razor blade.

MichaelG.

My worry too. I need to re-read my books because my memory is terrible, but I don't recall any of them discussing the optimum length or strength of a suspension spring. I assumed the spring should simply be strong enough to support the weight of the bob, and noted that spares sold for big clocks mostly look short compared with their pendula. (Pic from Cousins) I was also keen to reduce the amount of temperature sensitive metal in the pendulum by not exposing more spring than necessary.

I haven't attempted to measure Q yet. If a 0.1mm ( 0.004" ) razor blade is too thick, I could sand it down. Should be easy enough to Dremel out a slot as well. My authorities aren't keen on silk suspensions in high performance clocks, I guess because threads don't resist twisting as well as a blade spring. The more I get into clocks the more I find I don't understand.

Beyond simply lightening the spring, does anyone know what needs to be done to optimise a pendulum spring suspension?

Dave

Edited By SillyOldDuffer on 28/11/2022 10:09:59

[Robert Atkinson 2Participant @robertatkinson2]

I hope you are not testing it sat on the windowsill…..

[Michael GilliganParticipant @michaelgilligan61133]

Posted by SillyOldDuffer on 28/11/2022 10:08:14:

[…]

My authorities aren't keen on silk suspensions in high performance clocks,

.

Did you notice that I used the words “As a quick check …” Dave ?

Also [with the greatest respect] … You don’t currently have a high performance clock there.

MichaelG.

[BazyleParticipant @bazyle]

I'm not an Arduino user recently so don't know how you might be measuring period but are you using a RTOS mode and if it is saving or outputting results how does it do that without affecting the measurement. The existence of two period peaks implies one with and one without an extra interrupt routine. Bit like the LinuCNC timing problem on unsuitable computers.

[Michael GilliganParticipant @michaelgilligan61133]

.

This crams a lot of good stuff into its 145 pages

MichaelG.

[SillyOldDufferModerator @sillyoldduffer]

Posted by Andrew Johnston on 27/11/2022 20:35:13:

How do you know that the Arduino Clock Cycle is accurate and stable? A quartz crystal probably won't vary enough to give the results seen. But they do drift, usually 50 to 100ppm at the lower cost end. Stability is also dependent on the quality of the oscillator. Presumably there is softare between the crystal oscillator and the measurement being made?

AND

Apart from Andrews comments re the reference, if this is the first period of running, could it be due to changes in the flexture? Either work hardening or fatigue. I guess use as a pendulum flexture was not on the razor designers mind when the chose the steel for the blade.

On references, how do you know the Arduino crystal is 15.998101 MHz? The crystals used for microcotrollers are not known for their accuracy.
Confession, I'm a bit of a electronics "time nut" with 6 GPS disciplined oscilators / clocks, half a dozen Rubdium atomic oscillators, several high performance crystal ocillators, counters to 20 picosecond resolution and frequency difference measurement to better than 1 part in 100,000,000,000. I normally have 3 references running.

Robert G8RPI.

Good questions. The microcontroller is a Sparkfun Pro Micro, a miniaturised version of an Arduino Leonardo. It comes with a quartz crystal rather than a cheap unstable ceramic resonator. However, the crystal is an ordinary 50 – 100ppm type, there's no capacitor, and I've made no attempt to stabilise the temperature.

The microcontroller measures the number of crystal ticks per swing and for best resolution this is mostly done in hardware. The 16MHz system clock feeds a hardware counter triggered on/off by the pendulum blocking an IR beam. The counter is zero at start and on overflow, it clocks another counter. When the off signal is received both counters are frozen and a simple sum gives the total number of crystal pulses per swing. As the counters run at 16MHz, the pendulum is measured in ticks of about 0.0625 microseconds, considerably better than doing the same in software (worse than 4 microsecond resolution.) Accuracy depends on the quartz crystal, which of course could be wrong by 100 parts per million, and is temperature sensitive.

The same counter technique can be used to measure the actual frequency of the crystal. Substituting the seconds pulse output of a GPS module for the pendulum, the microcontroller counts the number of oscillations made in one second. This can be repeated and averaged.

In the clock, during the 0.8s between swings, environmental data is read, and everything logged to a Raspberry Pi3B.

The data is:

13432949 0.7461 200 0 994.76 81.29 14.87 836040 1669630663 148802507

Tick Count – 13432949
'Amplitude' – 0.7461 (actually a measure of how fast the pendulum is swinging, used to decide if an impulse is needed)
Pulse – 200 How long the magnet is switched to impulse the bob
Power – 0 (false) Whether or not the magnet was impulsed.
Pressure – 994.76mb
Humidity – 81.29% Relative
Temperature – 14.87°C
Nominal Clock Period – 836040uS. The uncompensated period used by the stand-alone clock. (Should be 835650)
Clock Time as UNIX Timestamp – 1669630663. Number of seconds since 00:00:00GMT 1/1/1970
Clock Time UNIX subseconds – 148802507. Fractional part of UNIX timestamp.

In the current set up I'm measuring the crystal's average frequency by comparing it with Network Time. The Raspberry Pi3B is connected to the internet and synchronises using NTP every 38 minutes. It timestamps log data on receipt, making it possible to compare pendulum clock time with network time, but otherwise has little else to do that might interfere. The arrangement isn't brilliant, but the Pi3B's notion of time is always better than 0.1s accurate, making it suitable for long-term comparisons. The number of crystal ticks counted over several accurate hours gives the frequency. I should also analyse the data by time slots, to see how the average frequency alters hour by hour.

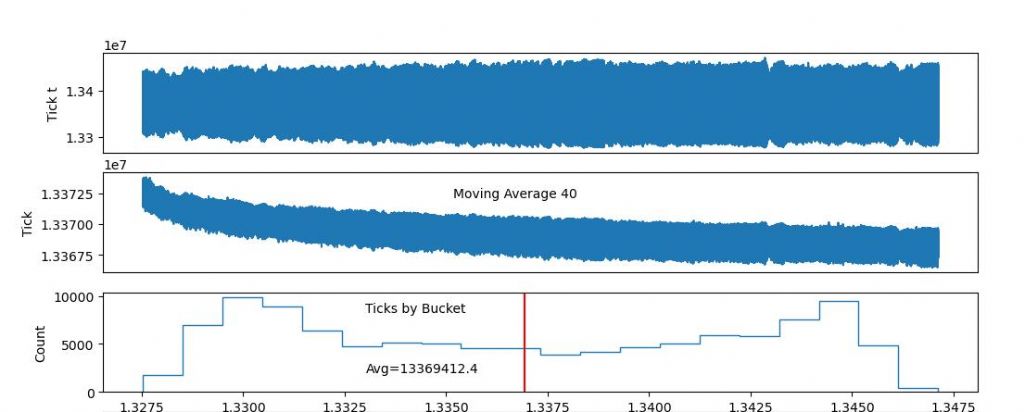
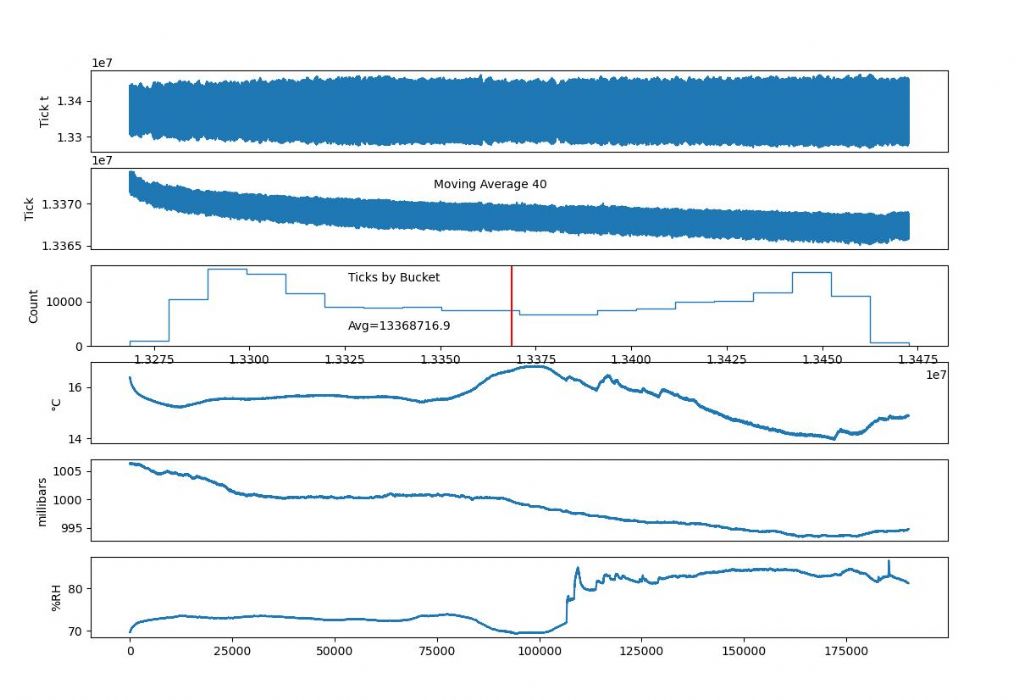
Until this morning, results suggested the experimental clock wasn't sensitive to the environment, but today suggests it could be tracking air-pressure. In the graphs below, the moving average falls with the millibar line until this morning when both lift together. Far from conclusive! I need to let the clock run for a lot longer.

I'm flummoxed by the shape of the 'Ticks by Bucket' graph. Next job is to check my code for the fifth time! Maybe I've misunderstood matplotlib or messed up the analysis. Otherwise I can't imagine how a pendulum's period could vary like that.

Robert's point about this being the first period of running is good. Although the clock has been run several times to test it and the software, they were all short runs. This is the first long one and perhaps it's shaking down. If so, it's taking a long time!

Let Robert's confession to being a 'time-nut' be a dire warning to others. The pursuit of accuracy time is addictive. I'm wasting lots of time on this and lust after Rubidium too…

Dave

[SillyOldDufferModerator @sillyoldduffer]

Posted by Michael Gilligan on 28/11/2022 10:20:55:

Posted by SillyOldDuffer on 28/11/2022 10:08:14:

[…]

My authorities aren't keen on silk suspensions in high performance clocks,

.

Also [with the greatest respect] … You don’t currently have a high performance clock there.

MichaelG.

I know, that's the problem…

[SillyOldDufferModerator @sillyoldduffer]

Posted by Robert Atkinson 2 on 28/11/2022 10:11:43:

I hope you are not testing it sat on the windowsill…..

Guilty. It's in an unoccupied north facing bedroom, and mostly safe from the cat. Where's the best place in an ordinary semi for a sensitive clock? Under stairs?

Dave

[Peter Cook 6Participant @petercook6]

Dave,

One way a pendulum could appear to behave like that is if it is slightly off vertical (out of beat), and you were comparing the timing of the left-right swing with the right-left swing.

Looking at the numbers (0.86sec period = about 180mm pendulum length), it seems that you are correctly counting full cycles, i.e. left-right-left.

If you are, then you need to drop the next left-right transition before starting the cycle again otherwise your system or code could be alternately timing left-right-left, and right-left-right which could give you the results you are getting.

PS a second thought – could the pendulum with its spring and flexible rod be behaving as a double pendulum. They do weird things! In regular clocks the pendulum rod is very rigid compared to the suspension spring. Sorry my math is not up to analysing a double pendulum.

 

Edited By Peter Cook 6 on 28/11/2022 13:52:35

[Peter Cook 6Participant @petercook6]

Dave – sorry – I got myself confused between positions and transitions – but the idea of the pendulum being out of beat stands.

[SillyOldDufferModerator @sillyoldduffer]

Posted by Peter Cook 6 on 28/11/2022 15:24:16:

Dave – sorry – I got myself confused between positions and transitions – but the idea of the pendulum being out of beat stands.

Best suggestion yet! I need to look at the program to see if it's possible, and if so what to do about it.

Just back from a hospital visit and found there was a power cut whilst I was out. My plan to let the clock run for a few more days has crashed and burned.

Never mind, it's an opportunity to move the clock off the windowsill and tweak the code again. Maybe I should install battery backup too!

Dave

[jaCK HobsonParticipant @jackhobson50760]

How is the pendulum support located?

There seems to be a correlation between pressure and period – so try sucking the air out.

The perfect pendulum doesn't involve a spring at all. Any hint of a spring gets it further from perfect doesn't it?

You want the suspension to be very much stiffer in every direction other than where you want it to swing. And not stiff at all in the direction of swing. Thinner section, but wider suspension.

You can get very good time keeping by having a mechanism to adjust for air differences rather than trying to eliminate the air. But I can see eliminating air is a fun project.

I think you should get a better RTC. I think you can get much better ones that the arduino for peanuts.

[John HaineParticipant @johnhaine32865]

One thing that occurs to me is that the suspension seems to permit movement in only one direction. If the axis of the upper part is not dead vertical and in line with the rod axis, the spring may be buckling slightly which could couple energy to other modes. Ideally one has a trunnion at the top of the spring that allows back-and-forth movement with some friction for damping but low stiction is possible; then the spring to allow side-to-side (the wanted mode); then often a second back-and-forth trunnion at the top of the rod.

As here, the top one being a screwed rod with ends turned down to smooth cylinders resting in vee- or u-shaped grooves in the bracket; then a double spring which inhibits twisting motion; then a screw for the lower trunnion but the lower spring chop is free to move in the gap. Thus the spring tension is along its axis. As well as possible buckling, maybe your rather narrow spring allows some twisting?

[Peter Cook 6Participant @petercook6]

Dave, there is an interesting simulation of a Double pendulum at Double Pendulum (bestofallpossibleurls.com)

If I set Mass1 and Length 1 to the minimum, and Mass 2 halfway and Length 2 about three quarters. Then set Phi & Theta to values that put the two rods in a straight line about 10 degrees off vertical to give the initial impulse, then the main bob looks like a simple pendulum, but it looks as if the period varies. The bob certainly does some odd things.

I think what you are seeing (assuming the code is OK) is the pendulum behaving as a double pendulum with the suspensions spring as one flexible point, and the pendulum rod itself as the other.

Reducing the stiffness of the suspension spring should help as the pendulum rod itself is probably bending as the suspension spring "stiffens" as it bends.

Edited By Peter Cook 6 on 28/11/2022 18:34:05

[duncan webster 1Participant @duncanwebster1]

Is a flexible pendulum called a bendulum? I'll get my coat

[Michael GilliganParticipant @michaelgilligan61133]

Dave

You may be interested in this:

I have just opened the December issue of the Horological Journal … Starting on p507 is a 4.5 page article entitled ‘A precision Internet-Connected Clock Timer’

The authors are engineers at Chronova Engineering Ltd.

**LINK**

https://chronova-engineering.square.site

MichaelG.

[Author]

Posts