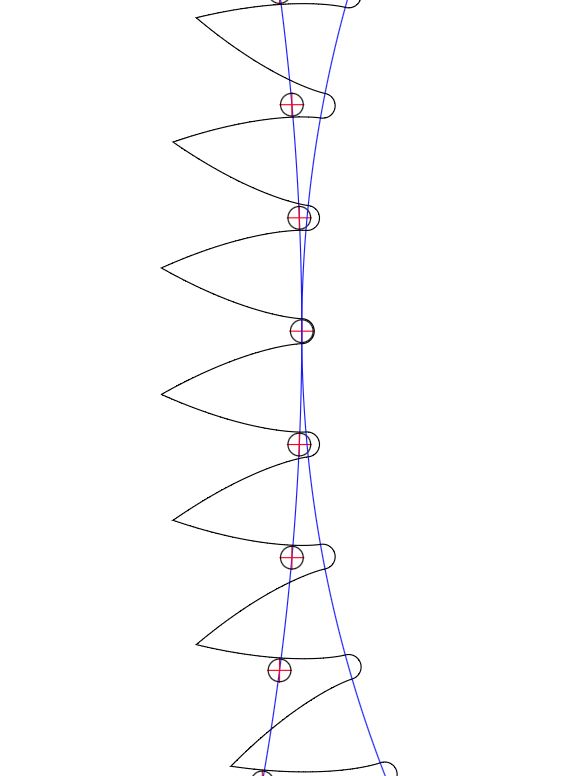
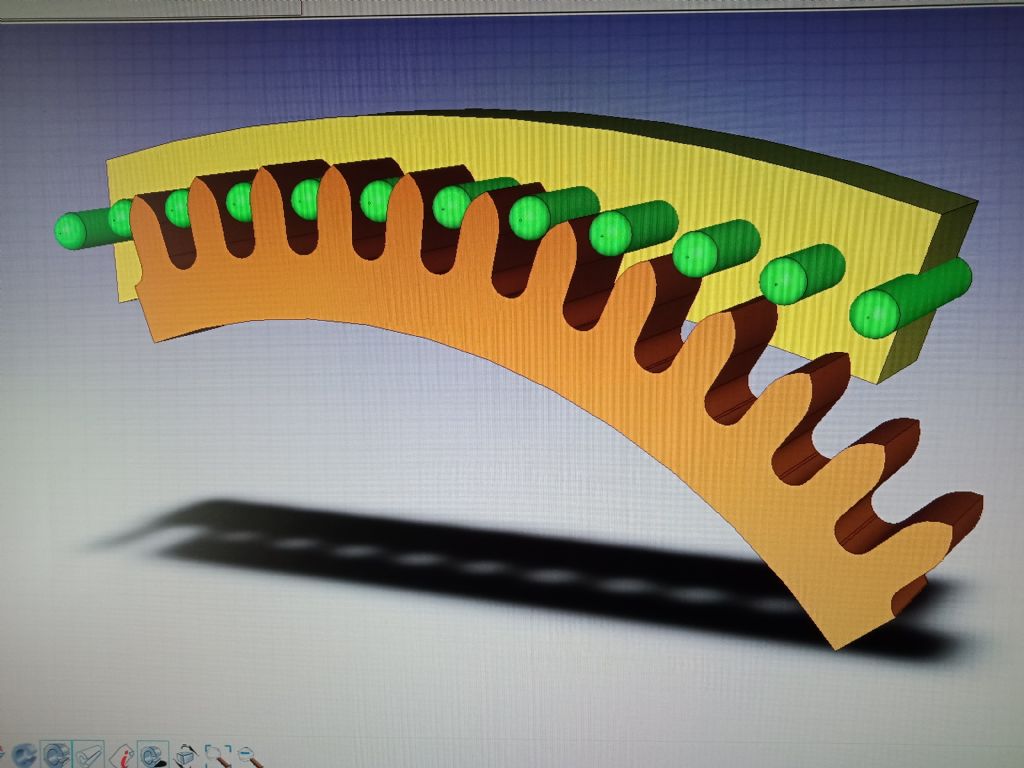
Epicyclic Clock
Epicyclic Clock
- This topic has 32 replies, 9 voices, and was last updated 5 November 2022 at 10:59 by
John Haine.
- Please log in to reply to this topic. Registering is free and easy using the links on the menu at the top of this page.
Latest Replies
Viewing 25 topics - 1 through 25 (of 25 total)
-
- Topic
- Voices
- Last Post
Viewing 25 topics - 1 through 25 (of 25 total)