Cycle chain drawing

[Peter G. ShawParticipant @peterg-shaw75338]

Hi all,

I am in the process of drawing a modification which uses a cycle chain. For my purposes, all I need is the side view of one of the outside plates. I have managed to do it by trial and error, but remain convinced that there should be a method using geometry, but unfortunately my GCE & C&G Maths along with investigations on the internet have not revealed a way of doing it. So, any ideas?

The sketch above shows at the bottom the desired shape, and above the basic method I have used along with the three known dimensions.

It seems to me that in order to get a smooth transition from the convex curve of the two circles to the concave curve of the dotted arc, the junction of the curves must be tangential to each other. Similarly, the 4.5 dimension being the dimension across the narrowest part of the plate must also be a tangent. In other words, what I need is how to construct a larger diameter circle which is tangential to both of the two smaller circles and a straight line at the narrowest part of the plate.

Over to you.

Peter G. Shaw

ps. As I said, I have done what I want by guesswork so this is now purely for interest.

[Peter G. ShawParticipant @peterg-shaw75338]

[duncan webster 1Participant @duncanwebster1]

The easy way is to use the ttt command in CAD. This gives a circle 13.66 diameter centred 9.08 from the centreline.

Otherwise I think you are into Algebra rather than Geometry.

call the radius ofyour big circle R. The distance from centre of big circle to chain pin is (R+4.25) From centre of big circle to centre line between pins is (R+2.25), so by Pythagorus (R+2.25)^2 + (12.7/2)^2 = (R+4.25)^2 which can be easily solved as te R^2 terms cancel out.

[JasonBModerator @jasonb]

Easy with CAD

[HOWARDTParticipant @howardt]

The circle command is TTR, tangent-tangent-radius.

[Peter G. ShawParticipant @peterg-shaw75338]

I knew there would be an easy way! I think the last maths I studied was way back in 1966 or thereabouts and other than the formula for capacitor charge/discharge, I haven't had to do any serious maths since then. Crikey, 52 years! Where has the time gone!

Duncan,

I haven't got a ttt command in my CAD (DesignCad Pro 3D). I do have a "circle tangent to three lines" command, but it always draws a small circle between the two 8.5 circles. Which of course is correct, but it's not the one I want.

Other than that, thankyou for the algebra. I've checked it out, and now understand it.

Jason,

Sorry to say that I don't understand your drawing. Obviously I understand it provided I already know all the dimensions, but I can't see how to discover the missing dimensions from it.

Howard,

Neither do I have a ttr command.

Thanks to one and all.

Peter G. Shaw

 

Edited By Peter G. Shaw on 18/09/2018 21:13:42

[Alan VosParticipant @alanvos39612]

I think I have it by constructed geometry. The resulting diameter* matches JasonB's algebra. Creating a nice looking 'Points A B C D E etc.' drawing will take a bit longer,

* Using F360, but traditional methods.

[duncan webster 1Participant @duncanwebster1]

Posted by HOWARDT on 18/09/2018 20:42:53:

The circle command is TTR, tangent-tangent-radius.

But you don't know what the radius is, you need ttt

[JasonBModerator @jasonb]

I don't have these TTT or TTR functions either and did not know the diameter of teh large circle.

What I did was draw the two 8.5mm circles 12.7mm apart, Then drew a guide line 2.25 (half the 4.5) above their ctr line and another guide line vertically between the two circles. Next I drew the third unknown circle starting with it's ctr on the vertical line and stopped when my mouse touched the left 8.5mm circle which set it at a tangent to this and the other one but it did not reach the 2.25mm line. So I then just used the tangent function to also make the large circle a tangent to teh 2.25 line.

As I did this the large circle altered it's own diameter and therefore it's ctr height this gave me the two unknowns. If you want a few screen shots of the various stages just ask

Edited By JasonB on 19/09/2018 07:09:11

[Gary WoodingParticipant @garywooding25363]

In TurboCAD there is a "Circle tan to Entities" command.

The attached was done by…

1. Draw a 12.7×2.25 rectangle

2. Draw two 8.5 diam circles with centres at the lower two corners of the rectangle

3. Draw a Circle tan to entities circle and choose the the two circles and the rectangle.

[John HinkleyParticipant @johnhinkley26699]

Peter,

Looks like you're sorted now, but my solution to this sort of problem is to go to:

**LINK**

and download a ( free ) 2D/3D file of the part I need. For example, this chain link pair was used in one of my sadly now lost projects. It's a dxf file, but also available in a multitude of other formats, including stl, etc. :

This just happens to be a chain link with 8mm between centres. ( I've added the dimensions below for illustrative purposes ). I have no reason to re-invent the wheel for each standard component when I can get a professionally drawn one so easily. Need a different size? Just use the scale tool.

My ½p.

John

[Perko7Participant @perko7]

Old school geometry would probably solve this as follows:

Using the centres of your two circles, draw arcs having a radius equal to the distance between the centres of your circles so that they intersect.

The intersection point is the centre of your new arc which will link your two circles. Draw lines from the intersection point to the centres of each of your two circles. Where these lines cross the boundary of your two circles will be the tangent points.

Using the intersection point as the centre, draw the arc linking the two tangent points.

Probably easier to draw than describe, refer sketch below. The orange line will be your required arc.

[Peter G. ShawParticipant @peterg-shaw75338]

Hello all,

Well, I never expected all these responses. Many thanks to all who have contributed.

One of the problems is that some of you are quoting CAD commands which simply do not exist in my program: to repeat, I use DesignCad pro 3D v.17.2 which dates from 2006 or thereabouts. This version is obsolete, but it generally does what I want, and usually, if it it doesn't do it straight away, I can calculate, devise, whatever, what is required, hence posing my original question as I did.

Just to forestall the obvious, I am using this program via Wine on Linux Mint, and whilst it is not perfect, it's about 97% there, and it mainly does what I want. Someone has managed to get v.24 working in a similar manner, but my understanding is that there has been a change of some sort around the v.25/26 mark, I think from 32bit to 64bit, but so far no-one seems to have got anything higher working. What this means is that buying a higher numbered version, at the price the program is, starts to become very risky for my situation. To put it bluntly, I'm not about to throw £100+ away on a program that might not work on my setup, especially when v.17 works as well as it does. If I could find a pukka, ie not the trial, version of v.24, then I might be tempted, but so far, they appear conspicuous by their absence.

There is another factor – my age. I'm in my mid-70's, and with not much desire to learn new software. Ok, a lot of the existing stuff should be ok, but I do know that there have been some changes.

Incidently, the question of a Linux version of DesignCad does keep arising on the DesignCad forums, usually after yet another cock-up from Microsoft.

Jason,

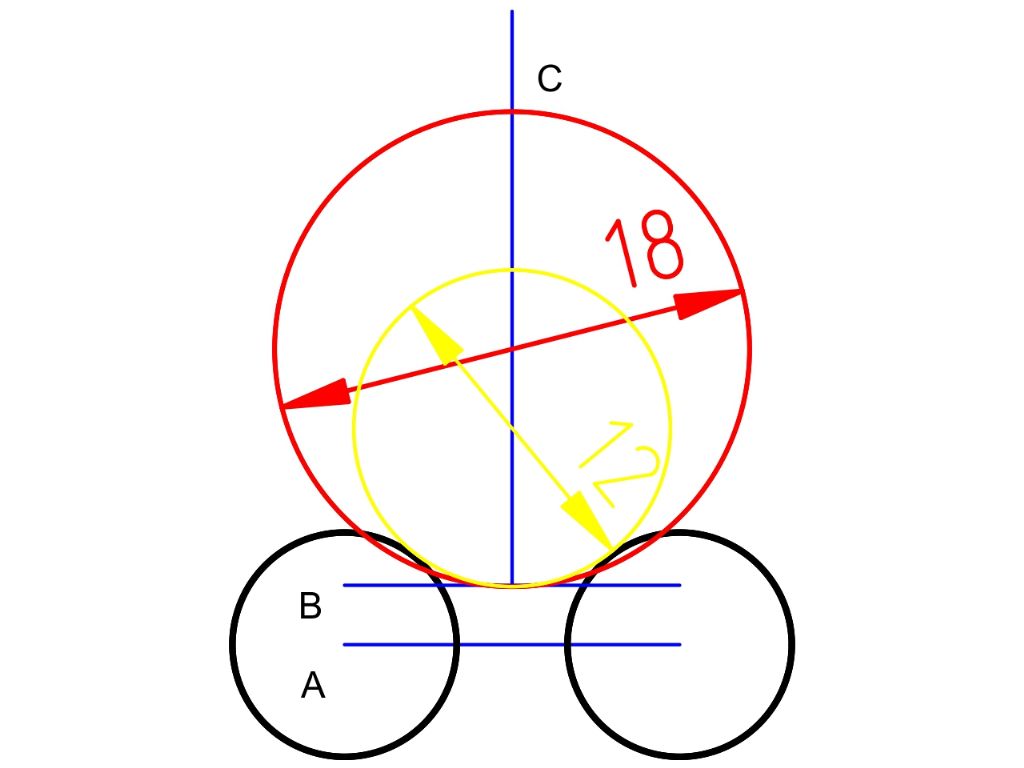
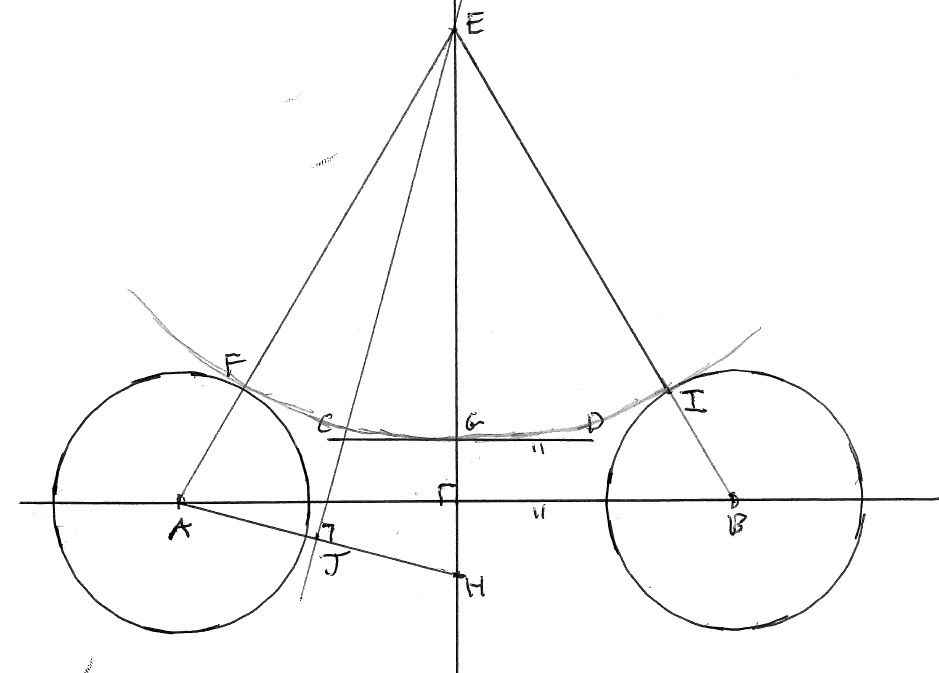
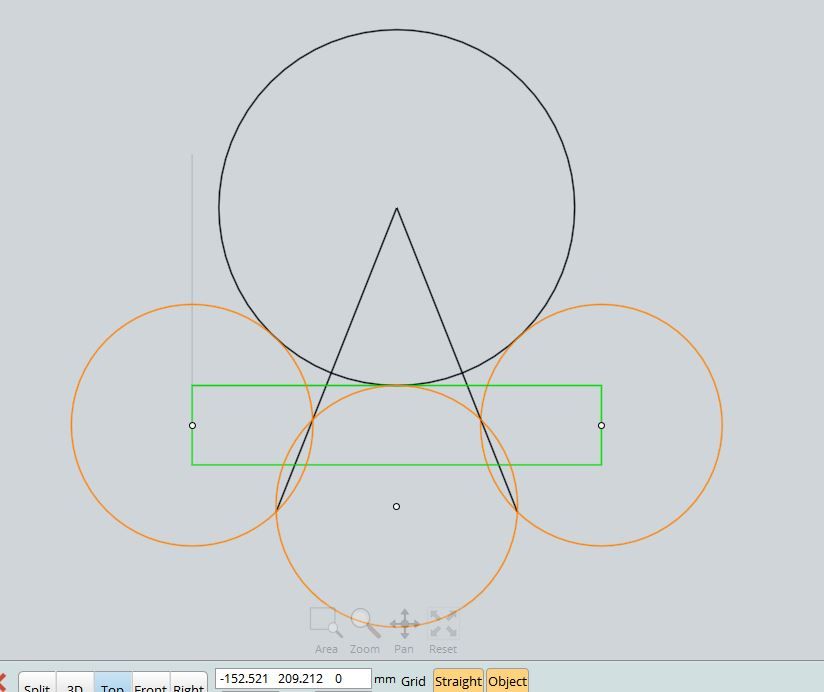
Your method is similar to what I eventually did.

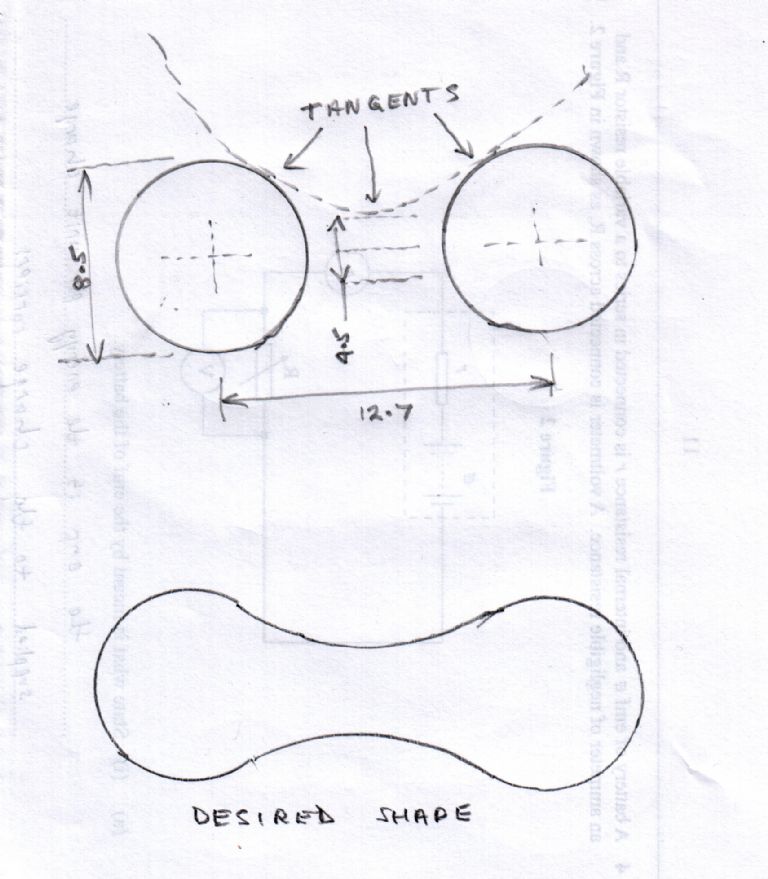
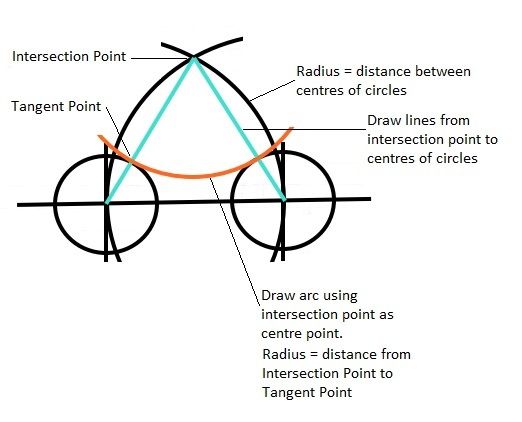
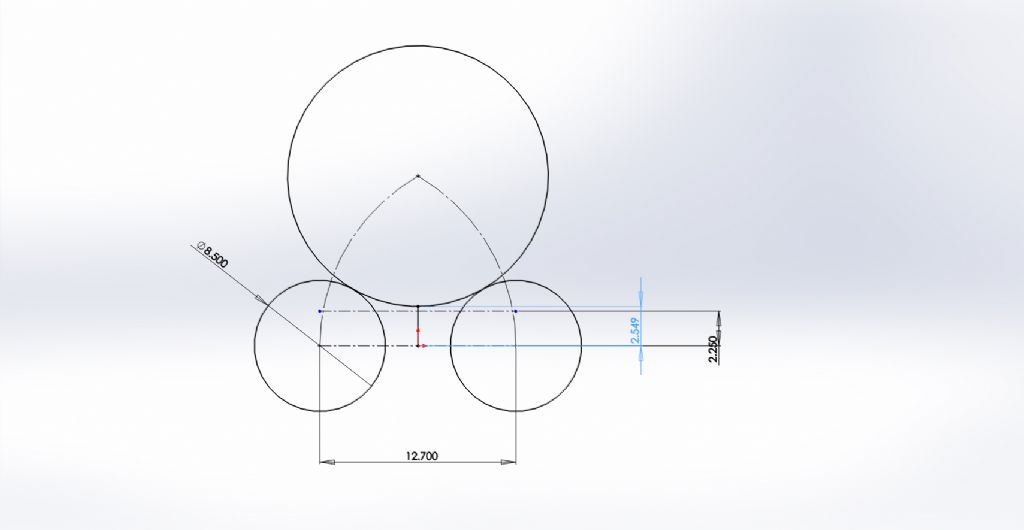
I drew the two smaller circles, correctly sized & spaced, then the two lines to represent the 4.5 gap in the centre. I then used the circle command to draw a large circle, and kept on adjusting until the circle appeared to be tangent to the smaller circles and the horizontal line. Next I used the Section Trim command to remove a portion of the smaller circles, and followed up by using the Trim command to cut out the unwanted part of the smaller circle and merge into the larger circle smoothly. The beauty of this command is that it will not do the trim if the two objects are not touching, hence I used this to determine whether or not to redraw the large circle until the Trim command worked. Messy I know, but it worked.

John,

I did indeed look on the internet for a drawing to use, and found plenty to copy, but not that particular file. Those that I did find, I tried all ways up to get into my drawing and failed. I even tried, with some success, to trace an original, however, in the end I went for a direct construction. I have checked with DesignCad and it does indeed allow imports of DXF drawings, so that's something to put away for next time. Many thanks.

Perko7,

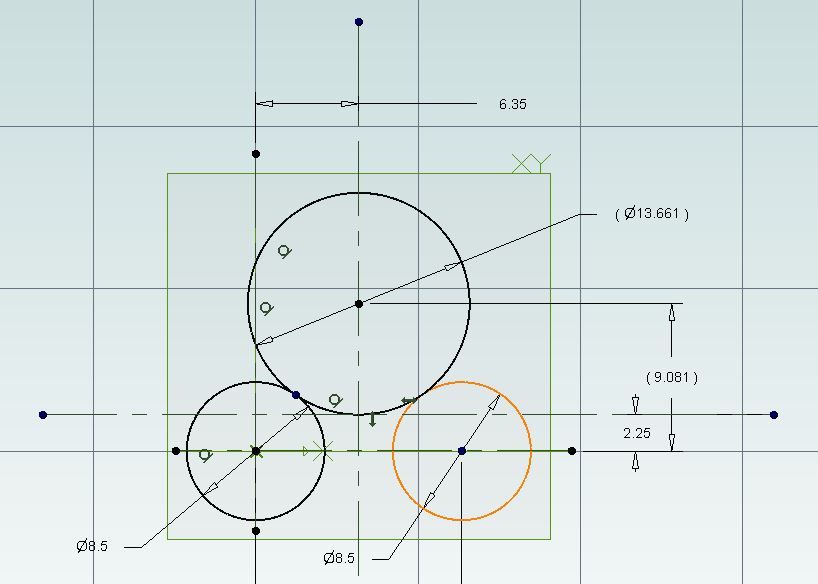
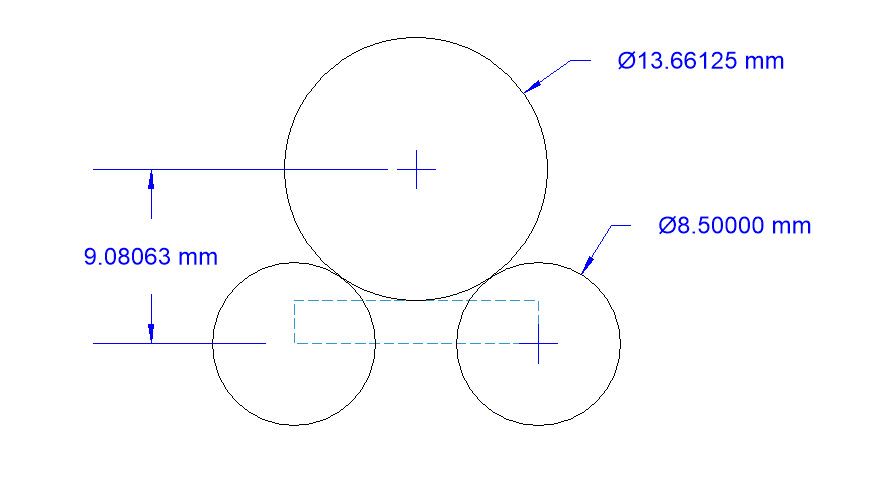
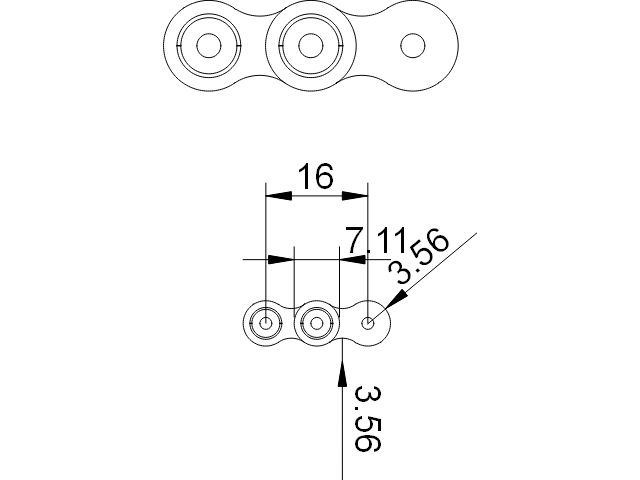
Thanks for that. Unfortunately it fails to take into consideration the third tangent, ie the one to the horizontal line 2.25 above the centre line between the two lower circles. In the grand order of what I'm doing in all probability that doesn't matter – except that I took my measurements from an existing chain, and tried to meet them which turned it into an intellectual exercise. Like you, though, I thought old-school geometry, but as someone has said, it's actually algebra as well (actually I suspect more trigonometry, but hey-ho).

That's all folks,

Peter G. Shaw

 

Edited By Peter G. Shaw on 19/09/2018 10:28:24

[Phil PParticipant @philp]

Perko7

Unfortunately your method does not work out in practice, it sort of looks OK but it leaves the middle thickness at 5.098mm which is much thicker than the OP's desired 4.5mm.

I was curious to see if your method worked and plotted it out in Solidworks 3D CAD to test it.

Sorry to pull the rug.

Phil

Edited By Phil P on 19/09/2018 10:22:28

[Neil WyattModerator @neilwyatt]

The problem is that everyone is either making it too complicated or offering solutions that don't fix the diameter tomeet the horizontal line.

Crop or resize the rectangle so that it ends half-way between the two circles.

Draw a tangent arc between the corner of the rectangle and one circle.

Repeat for the other side.

Simples.

Neil

[Ian PParticipant @ianp]

Even simpler in AutoCad which has 'circle by three points'. The three points all being tangents. (to circle 1, to circle 2 and to the line at the specified height).

Ian P

[JasonBModerator @jasonb]

I think the problem is we all use different CAD packages be they 2D or 3D and each has its own way of doing things, I don't have Neil's "tangent Arc" for example or at least not by that name. So what may seem over complicated to a user of brand X is just a couple of simple clicks for the user of brand Y who knows their own particular package.

With such an old program it is also less likely to be able to import some files off the net, I doubt STEP files were even about in 2006 for example.

Edited By JasonB on 19/09/2018 11:00:24

[John HinkleyParticipant @johnhinkley26699]

Peter,

You have a PM.

John

[blowlampParticipant @blowlamp]

Posted by Neil Wyatt on 19/09/2018 10:26:17:

The problem is that everyone is either making it too complicated or offering solutions that don't fix the diameter tomeet the horizontal line.

Crop or resize the rectangle so that it ends half-way between the two circles.

Draw a tangent arc between the corner of the rectangle and one circle.

Repeat for the other side.

Simples.

Neil

I can't visualise what you mean.

Martin.

[SillyOldDufferModerator @sillyoldduffer]

Easy enough to do in QCAD, which has similar tools for drawing circles and tangent to those described with other drawing packages.

Peter said in his opening post 'I have managed to do it by trial and error', which is not to be despised. It may even have been how the first chain link was drawn by a draughtsman. An approximate result is often 'good enough', especially if it also simplifies production.

With compass, set-square and paper you can get close by simple trial and error in a few minutes.

1. Draw construction line A, 12.7mm long

2. Draw construction Line B parallel to and 2.25mm above line A.

3. Draw construction Line C vertically from the centre of Line B

4. Set the compass to a largish radius, I guessed 9mm, and draw a circle aligned to Line C with the pencil touching Line B. By inspection it can be seen that the resulting red circle overlaps.

5. Set the compass to a smallish radius, I guessed 6mm, and draw another circle aligned to Line C again with the pencil touching Line B. By inspection it can be seen that the resulting yellow circle is slightly too small.

6. Repeat steps 4 and 5 altering the radius setting of the compass slightly step by step until the resulting circle fits.

Drawn actual size the cycle-link is rather small. A more accurate result is obtained by multiplying the dimensions by 10.

In this simple requirement the advantage is not having to learn a CAD package!

Dave

[Alan VosParticipant @alanvos39612]

I believe this works. The key is making GH equal to the radius of the two circles.

AB is the line between the centres of the two circles
CD is the defined line, parallel to AB
E is the centre of the desired circle

Construct the perpendicular bisector of AB, this intersects CD at G)
Construct H such that GH=AF=BI
Construct the perpendicular bisector of AH
Those two perpendicular bisectors intersect at E
The desired circle has radius EF=EG=EI

As a check, construct the perpendicular bisector of BH, which should also pass through E.

[blowlampParticipant @blowlamp]

A similar solution to that of Alan Vos

[duncan webster 1Participant @duncanwebster1]

Posted by Alan Vos on 19/09/2018 17:57:20:

I believe this works. The key is making GH equal to the radius of the two circles.

AB is the line between the centres of the two circles
CD is the defined line, parallel to AB
E is the centre of the desired circle

Construct the perpendicular bisector of AB, this intersects CD at G)
Construct H such that GH=AF=BI
Construct the perpendicular bisector of AH
Those two perpendicular bisectors intersect at E
The desired circle has radius EF=EG=EI

As a check, construct the perpendicular bisector of BH, which should also pass through E.

Neat, making 2 equilateral triangles. Wish I'd thought of that

[Author]

Posts