Constrained Pendulum and Earth Rotation
Constrained Pendulum and Earth Rotation
- This topic has 52 replies, 17 voices, and was last updated 7 February 2017 at 16:06 by
Geoff Theasby.
- Please log in to reply to this topic. Registering is free and easy using the links on the menu at the top of this page.
Latest Replies
Viewing 25 topics - 1 through 25 (of 25 total)
-
- Topic
- Voices
- Last Post
Viewing 25 topics - 1 through 25 (of 25 total)
Latest Issue
Newsletter Sign-up
Latest Replies
- taper pins
- Measuring increments on boring head
- Myford Super 7 restoration problem.
- Half Scale 1/4HP A J Weed Engine
- Autodesk Fusion Discount
- DIY Pendulum Timer – GPS-Synced Beat Analyser
- Steam pressure using thermistor
- Damp proofing concrete floors
- Contact Details for the family of Alan Barnes
- Myford saddle lock issue



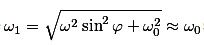
 Neil
Neil


