benchtop power supply

[Steve GarnettParticipant @stevegarnett62550]

For the 2v supply, you could use something like the circuit we were discussing on page one, only using a MIC29152WT variable regulator. This gives 1.5A at voltages down to 1.25v. I’m sure that those valve heaters aren’t that hungry! If I recall correctly, it’s only around 25mA per valve they need.

[Les Jones 1Participant @lesjones1]

Hi Ian and Steve,

I was going to suggest more or less the same solution as Steve as one of the possible solutions. (Assuming you want to power it from the mains and not a set of nicad cells etc.) I was thinking of using a 6 volt transformer which would be rectified, and regulated for the 2 volts with an LM317 regulator. (A switching regulator would be better but more complex as a linear regulator would have to dissipate more power than used by the valve heaters.) I think the valve heaters use about 200 mA each. I remembered the type of valve I used when I was a child to build a radio control receiver for a model boat. It was a “PM2” and I found the heater current from the web. For the 135 volts the 6 volts AC from the first transformer would be stepped up to about 100 volts AC the way Steve suggests which when rectified and smoothed would give about 140 volts DC. A transformer rated to give about 13.5 volts when used normally would give the correct voltage but the nearest you would find would be 12 volts. Another solution for the 135 volts would be a 24 – 0 – 24 transformer with a voltage doubler used in the normal way. Probably the cheapest way to get capacitors for smoothing the 135 volts is from the cheap low energy bulbs you sometimes see being sold for about 10 P each.

 

Les.

[Steve GarnettParticipant @stevegarnett62550]

Well if it’s a Bush portable and it uses the D series valves, most of them take either 25 or 50mA for the heaters, and even the output valves only take 100mA. What intrigues me slightly though is that these are all 1.4v heater devices. A typical late example is the Bush BP61 – uses DK96,
DF96, DAF96 and DL96, and that means less than 200mA heater current in total. Which makes sense, because otherwise the L.T. battery life would have been truly awful.

 

Ian, exactly what’s the model number of yours? And are you absolutely sure it has 2v heaters?

 

Incidentally I should perhaps mention that I used to repair these damned things for a living, and still have some of the valves! Also, I found a website with portable radio power supply information, including a link to the quadrupler design, and actually that doesn’t look too bad. The page that links to it, and at least two more designs is here.

[Ian S CParticipant @iansc]

I made an HT power supply for a single valve battery set that I built years ago. It has an oscelator, 2 BC 108 , the output of these is fed into the secondry of a small power transformer, the out put from the transformer goes to a bridge rectifier, 2000uf capacitor, The open voltage is about 90 volts with a 9 volt input (The little 9V with the dome clips on top). The set uses a DAF 91. Not quite a workshop radio, its headphones only. Ian S C

 ps., LT is 1.5 v, so I just use a battery, either a C, or AA cell.

Edited By Ian S C on 14/09/2011 11:53:17

[ian weeks 1Participant @ianweeks1]

Thanks everyone , I I think I follow steve and les’ postings. Un fortunately I boobed in my first posting and referred to a ‘bush’ that is actually the old bush ac11 which is at my bedside having got in going about 10 years ago – even wife allows it as it’s cabinet is lovely wood! The battery job is an eko b53 !!–sorry ! [b53 135v/2v bush 90 or so /1.25 ]Had intended to do a bit on the gear box I’m slowly making for the myford tonight when I get home but think I’ll spend the time looking at the links mentioned and probable re -reading my old electronic primer- I think I know whereabouts it is in the attic!!!!!!!!! Thanks chaps -the avenues which one ends up going down are what makes this hobby so interestin regards Ian

[Donhe7Participant @donhe7]

Posted by ian weeks on 09/09/2011 23:31:52:

Dear All,

whist building the gear banjo in MEW issue82 I once again read the article in the same issue by peter rawlinson on electronics in the workshop. It took me back to the ‘radio and electronics club at school many decades ago.

I resolved to build the project at the end of the article as a ‘nostalgia trip’.

However I have a problem -the circuit shows 4 of the capacitors as 10 microfarad 35vw but the pictures show one of these as a physically much bigger beast of an electrolytic[ viz the one across the output of the bridge rectifier]. My problem is that a little bell is ringing in my head and saying that this capacitor should br bigger but my knowledge is so rusty I cant be sure and I can see no corrections to the circuit inn subsequent issues.

Any advice would be appreciated

Regards Ian

Whilst not having seen the article on the power supply project, in my experience with 7805s and similar regulators, the input voltage is best kept as low as possible while still high enough to not drop below the voltage of the regulator.

My own approach to the power supply situation is to use a large value electrolytic capacitor directly after the rectifier to give as smooth a supply voltage into the 78xx as possible to ensure that the ripple is virtually none existent and don’t forget any low value “greencaps” on both the input and output of the 78xx, to prevent possible oscillation, which I believe is possible without them.

 

donhe7

[Steve GarnettParticipant @stevegarnett62550]

Posted by Donhe7 on 14/09/2011 15:59:22:

 

Whilst not having seen the article on the power supply project, in my experience with 7805s and similar regulators, the input voltage is best kept as low as possible while still high enough to not drop below the voltage of the regulator.

 

The snag with this particular design as published is that it runs two regulators from a single supply, one of them being variable up to 20-something volts. So the poor old 7805 has to run from a relatively high rectified secondary voltage, because only a single secondary was shown. In an ideal world, this power supply would be better served with two secondary windings, rectifiers and reservoirs, and a much lower voltage feed to the 7805, as you suggest.

 

Ekco B53? Ooh, that’s old… uses old Mazda valves I haven’t got any of. But I found a service sheet for the radio, and you need 135v at 10mA (not much) for HT, but for the heaters, you do indeed need 2v, and best part of half an amp in total to run them. (0.41A, to be precise). Which is why, when it was originally sold, it came without an accumulator to run the heaters – you had to provide that yourself as an extra. At least you could recharge that!

[Les Jones 1Participant @lesjones1]

Hi Ian,

I found this web page with some information on your Ekco b53

Ekco B53 info

 

I think you have to join the forum to access the full information.

 

Les.

[Les Jones 1Participant @lesjones1]

Hi Ian,

Here is some more information on your radio.

 

Ekco B53 Site 02

 

Les.

[Steve GarnettParticipant @stevegarnett62550]

The one thing that’s likely to have dried out in the radio is the two electrolytic capacitors, C23 and C25. They are relatively easy to locate, because they’re mounted under clips. Because they won’t have a ridiculously high working voltage, equivalents are still available – well, 160v ones are with very similar values to those shown are, anyway. I’m not suggesting that you actually buy them from RS components, because they’ll make you pay for 5 or 10 of them, but to give you an idea of what you’re looking for, have a look at their part numbers 707-6521 and 707-6360.

[ian weeks 1Participant @ianweeks1]

Thanks Steve , just read the posting and I am getting Quite fired up at the thought of having a go . will be a few weeks yet before I have enough spare time but the preparation and reading will be fun.Slowly but slowly the nuts and bolts are coming back. The only problem is explaining to my wife why I’m not concentrating on getting the steam engine prepared for the church christmas fair Santa Specials!! If [when] I run into questions I know I can count on everyone for extremely knowledgable advice—Ian

[Donhe7Participant @donhe7]

Posted by Steve Garnett on 14/09/2011 18:57:40:

Posted by Donhe7 on 14/09/2011 15:59:22:

 

Whilst not having seen the article on the power supply project, in my experience with 7805s and similar regulators, the input voltage is best kept as low as possible while still high enough to not drop below the voltage of the regulator.

 

The snag with this particular design as published is that it runs two regulators from a single supply, one of them being variable up to 20-something volts. So the poor old 7805 has to run from a relatively high rectified secondary voltage, because only a single secondary was shown. In an ideal world, this power supply would be better served with two secondary windings, rectifiers and reservoirs, and a much lower voltage feed to the 7805, as you suggest.

 

Agreed about the “poor old 7805”, not an ideal situation.

Pity a multi tapped or multi secondary transformer could not be used, the other alternative would be to use the pre-regulated supply for the input to the 7805, if it is possible to do so.

 

With regard to the “battery valved” radio, there was a series about powering this type of equipment in an edition of an Australian “Silicon Chip” magazine some time ago, I think it was in the Historical Radio section, and if I recall correctly, used a transformer and voltage doubler circuit for the HT supply, but I cannot recall how the filament voltage was obtained.

 

donhe7

[Steve GarnettParticipant @stevegarnett62550]

It’s worth noting that it’s the filament voltage you need to be careful with here – that’s the one you don’t want to overdo – but there again, you don’t want to underdo it too much either.

 

The HT supply is considerably less critical. Many of these older radios ran quite well on significantly lower voltages than they were intended to. There were rumours that with some radios of this type, you could still get results with the voltage down to 20-30! Don’t think that they’d be very loud though.

[Gordon WParticipant @gordonw]

Why not do a full home workshop job? Make a lead acid battery and a vibrator to get the HT ? Sure there must be plenty of info. on t.net.

[ian weeks 1Participant @ianweeks1]

Dear All ,

Thank you all for your advice and help . Cruised past Maplins today and just had to stop. Between them and bits in the shed and attic nearly enough to make a start . the trouble is the reading and thinking bit is fun!! I have had a look at the ‘stennings’ circuit diagram and the LT circuit looks a goer for the required 2v[by adjusting the resistor values across the lm317]. Having taken on board your comments about the ht circuit and having 230v twin 24v output and 230v twin 18v output transformers in the spares [come in handy one day box] is the idea of using one of these as a ‘step’ up from the 15v seecondary winding a starter as per your earlier suggestion rather than the straigh’t voltage quadruple’ circuit shown? A. bearing in mind I’m a tyro and B. I would love to understand the voltage quadrupler circuit but don’t [ Am on amazon for a more modern primer tonight].also just thought If used 24v transformer totally seperately wouldn’t that get me pretty damn near required 138v using quadrupler circuit– then drop it -feel free to shoot me down in flames.

Thanks again Ian

Oh And another project has arisen -Have had a chester e30 mill for 2 years lovely little machine little use as I mainly use my Theil but noticed an irritating jerk on the x axis when milling My friend came round tonight and helped me remove table- no wear on screw or nut or tangential gibs -all pristine BUT would you believe the machined feed screw nut has no positive location just 2 capscrews wich allow lateral movement no locating peg or key -nut thread pristine – looks like a big job to provide a positive location for the nut and or a longer acme thread cutting and milling new purpose built nut. The words ship and ha’pence o’ tar come to mind !!– Ian

[ian weeks 1Participant @ianweeks1]

Dear All – following on from 5 minutes ago ??just use 24v for both circuits and adjust values of components before lm317 ?? I would probably get calcs wrong!-Ian

[Les Jones 1Participant @lesjones1]

Hi Ian,

I do not think using the 24 volt transformer for both HT and LT is a good idea. I you rectify 24 volts this will give you 24 x 1.414 (Root 2) which equals about 34 volts. With the volts drop due to the diodes in a bridge rectifier this will reduce it by about 1.4 volts so you will still have 32.6 volts. This will mean that the regulator is dropping 30.6 volts. As the total heater current is abut 0.5 amps the regulator will be dissipating about 15 watts. Using a switch mode regulator would solve that problem but would be likely to generate interference.

I suggest using the two 24 volt winding in series with a voltage doubler. This would give about 48 x 1.414 x 2 = 135.7 which is just about right. (It would probably be a little higher than this because the transformer would be so lightly loaded.) A separate 6 volt transformer would be about right to supply the heaters with the LM317 regulator. If you put a picture of the quadrupler circuit in your photos (Or a link to it.) I will try to explain how it works.

 

Les.

[Steve GarnettParticipant @stevegarnett62550]

If you have two transformers, one with 2 x 24 secs and one with 2 x 18v secs, run them both from the mains as per normal, but put all the secondary windings in series and multiply it by root 2 (aka 1.414), you end up with just under 120v – which is probably sufficient… but I don’t think I’d do it like that either! If I was doing this with transformers, I’d start with one that has, say, a 6v output and use that for the filament supply, and then get a 12v secondary transformer running backwards from the 6v one to give you approximately a sensible HT voltage requiring simple stabilising. Transformers to do this are easily available, and cheap – these are standard voltages.

 

All voltage doublers/triplers/quadruplers work the same way in principle. The basic idea is that you are rectifying the input voltage several times, and stacking up the resultant outputs. The basic idea is simple, but because the means of doing this uses charge pumps working on alternate cycles of AC, it gets a little harder to explain the overall action in a post here. I found a bit of google book that explains it though, and you can look at that here (scroll up and down a bit).

 

The quadrupler that most people refer to in this context is Paul Stenning’s one here which is presumably the one you found (the upper part). If you start with a higher voltage secondary (24v) and use 100v capacitors throughout you’ll end up with about the right value of HT, I think. The difference between this one, which looks a bit like a doubler and the ‘classic’ quadrupler is that this is a full-wave one – so it’s effectively two doublers in series – which explains how it looks!

[Les Jones 1Participant @lesjones1]

Hi Ian,

This explanation of how the quadrupler refers to the Paul Stenning design that Steve pointed to.

Think of the circuit as two voltage doublers. One giving a positive output with reference to the bottom end of the top 15 volt winding. The other giving a negative output with reference to this point. I will only explain the positive part a the negative part work in the same way.

Voltages in this explanation are with reference to the bottom end of the top 15 volt winding.

When the top of the winding is at its peak negative point on the wave form capacitor C1 is charged to about 21 volts (1.414 x 15) The positive end of C1 is clamped to 0 volts at this point in time by D2. When the waveform swings to the positive peak the negative end of C1 will be at about + 21 volts. As C1 is already charged to 21 volts the positive end will now be at about + 42 volts. D3 now conducts to charge C4 to about 42 volts. Both of these capacitors must be large enough not to discharge significantly in 20 mS. With the part of the circuit that gives the negative output we finish up with about 84 volts. As the negative output is connected to our 0 volt reference (Ground) the positive output is at + 84 volts with respect to this point.

I hope this explanation is clear.

 

Les.

 

[Steve GarnettParticipant @stevegarnett62550]

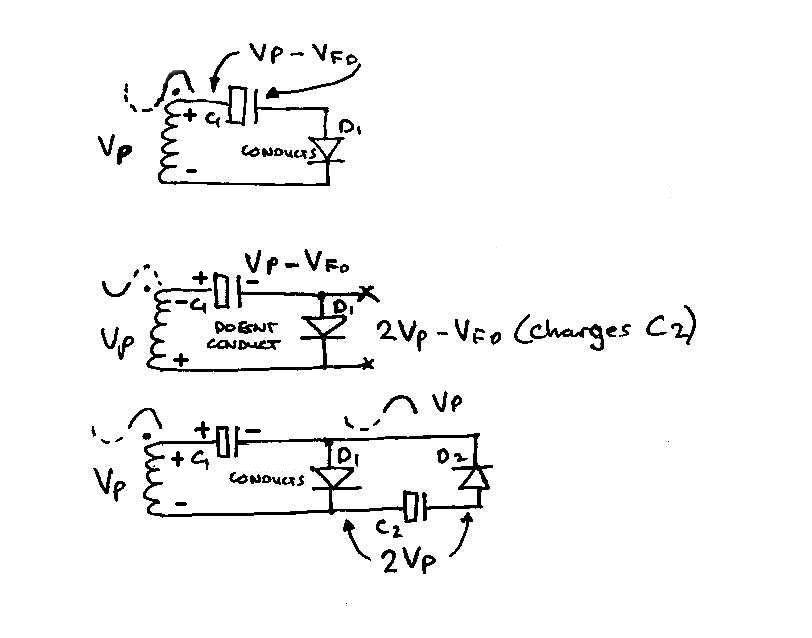
I’m not 100% convinced that the explanation given in the google book is that easy to understand, so here’s my take on it, FWIW. I apologise for the awful sketches!

 

On the first positive half cycle (sketch 1), D1 conducts, and C1 gets charged up to the peak voltage Vp (technically minus the diode drop, but we can effectively ignore that).

 

On the second, negative half cycle (sketch 2) D1 doesn’t conduct, but for half a cycle, you will see that the charge on C1 is effectively in series with the secondary, so that at the points x-x the voltage is now 2Vp. (Yes it’s still minus that diode drop but that’s only 0.7v or thereabouts.) You’ll now notice that the voltage has doubled.

 

In sketch 3, which we’ll call the next half cycle, D1 conducts again, recharging C1. You will note that because of the behaviour of capacitors to a rate of change of voltage, the pulses effectively pass through C1 and C2, and the same behaviour takes place again in the next two stages, with a resultant 2Vp appearing across C4 as well. This gives you two capacitors in series with 2Vp across each of them, so if you take an output with the +ve terminal on the + side of C1 and the -ve terminal on the – side of C4, you have effectively quadrupled the output.

 

The resultant output never makes it to the full Vp x 4, because any attempt to draw current will discharge the capacitors between half-cycles. And because the charge is based on the transfer of energy through capacitors, which have a very finite series resistance, the current available is pretty limited. Despite the claim, I don’t think that all of the diodes are likely to see 2Vp as a peak inverse voltage across them – probably only the first one in a real-life situation, but I haven’t checked that in detail.

 

That may or may not be easier to understand. Hopefully if you read it in conjunction with the book, it may all make some sense!

 

(Les posted his as I was preparing this one, but I’m pretty sure that even though the words are different, the explanations are essentially the same)

 

Edited By Steve Garnett on 16/09/2011 23:50:37

[ian weeks 1Participant @ianweeks1]

Thanks again chaps, Am off for a hill walk in rosedale this morning with my wife ,have printed off your replies and when we run out of things to say will mull them over-thanks ian

[Sub MandrelParticipant @submandrel]

Just a thought, lot’s of folks worrying about using 7805s with high currents and supply voltages (30V+).

 

The efficient alternative is a switch mode PSU. Now DON’T PANIC! There’s a chip, the LM2595, ‘simple switcher’ that is not much more difficult to wire up than a 78series and it is vastly more efficient (about 90%, I think, when a 7805 on a 30V supply is only about 18% efficient). The LM2595 comes in 5, 12 1and variable versions. The downside is you need a 68uH coil that can take 1A and a shottky diode.

 

Neil

[Steve GarnettParticipant @stevegarnett62550]

Hmm…. Might be quite interesting running that in a box next to a MW radio!

 

I’d already thought of using a small switcher, but decided that keeping it simple and linear might be better under the circumstances, although I must admit that I haven’t mentioned this up till now. But you’re right about the dissipation and efficiency, which is why I suggested using a 6v transformer to run the 7805, rather than the original 24v one, which is definitely OTT!

[ian weeks 1Participant @ianweeks1]

Thanks for all the info ,the walk was fantastic and thanks to your explanations I think I understand the voltage multiplication circuit. Just back in from the shed ,having plucked up courage and attempted the LT side of the Stenning design -the soldering is atrocious ,2 out of 10 for neatness and as I didn’t have the right value of resistor to hand made R6 18 R to give 1.36V. I am still recovering from the shock that it worked reading 1.345v on my meter. For you guys this must be kindergarten stuff but as I haven’t done anything like this for over 40 years I am walking on air.

Thanks again Ian

[ian weeks 1Participant @ianweeks1]

Dear All,

This should be titled’bench power supply —-almost’ Last night had some spare time and as I can’t get on with the radio supply till my order for 100v capacitors arrives decided to build the supply as detailed in MEW. Al went well LED lights /5v supply reads 5v but variable supply fries 180r resistor and when checked output is full 37v rectified dc I have checked the circuit wiring a dozen times and can’t find I’ ve done anything wrong [using chocolate box design as per magazine ] also if turn up Variable resistor makes expected ‘warm’ noises Any suggestions as to what I am doing wrong

Ian

 

 

 

 

 

 

 

 

 

 

[Author]

Posts