Arc tangent to two ellipses

[Ivan GinatoParticipant @ivanginato28142]

I’have been practining my board drawing skills and I can’t understand how to draw a arc tangent to two false ellipse. Could someone help my? Following the model drawing and my drawing:

Model drawing

My drawing

[Ivan GinatoParticipant @ivanginato28142]

Technical drawing

[Ivan GinatoParticipant @ivanginato28142]

I tried to draw the arc but it does not seem correct.

[Perko7Participant @perko7]

When I did my tech drawing training back in 1970, we were taught to draw it out in plan and elevation first, then draw construction lines at regular intervals perpendicular to the long axis which intersect the arcs. Then we could measure the offset and repeat that for drawing isometric or oblique views. The curve then became a freehand 'join the dot's as it rarely was a constant radius. Hope this helps.

[JasonBModerator @jasonb]

It's times like this when an isometric ellipse template comes in handy, it is actually 3 ellipses joined together that you need.

If not then as Perko says draw it out and construct a series of points then freehand the line between them.

 

Edited By JasonB on 11/04/2019 10:17:28

[SillyOldDufferModerator @sillyoldduffer]

This is how I did it.

First draw the centre lines and the 5½" line. Then draw (in yellow), a 4¾" construction circle on the centre, and a 1¼" construction circle on the end of the 5½" line.

Next draw a construction circle (in blue) on the centre line that's 2½" larger in radius than the objects 4¾" diameter, ie. 4.875". Add a second construction circle (in blue) on the 5½" line that's 2½" larger in radius than the 1¼" lower radius curve, ie 3.75".

The intersection of the two blue circles is the centre point of Ivan's required 2½" tangent curve:

Removing construction details:

Dave

[JasonBModerator @jasonb]

Dave, it's the isometric that Ivan is trying to draw (see his second link) hence the need for elipses.

Edited By JasonB on 11/04/2019 12:16:41

[SillyOldDufferModerator @sillyoldduffer]

Posted by JasonB on 11/04/2019 12:03:41:

Dave, it's the isometric that Ivan is trying to draw (see his second link) hence the need for elipses.

…

Oh dear, wrong again! Still, apart from that it was a good answer…

I shall have another think, this time with brain engaged!

Dave

[JasonBModerator @jasonb]

Well not quite wrong as you do need to be able to draw the plan as per your method to get the lines to project.

The other option is to again work out the middle of the circle that forms the concave side and then just construct the three circles on one plane as ivan has done for the central circle. You then just draw around the line that the 3 circles form to get the edge of the part.

[SillyOldDufferModerator @sillyoldduffer]

Ivan's problem highlights the advantage of 3D CAD over pencil and paper methods and 2D CAD. For example, QCAD has basic tools that allows the draughtsman to nudge shapes into isometric form.

The isometric lines are created by transforming and rotating the drawing. Might have a go at explaining the maths  but the number-crunching is quite involved.

Anyway, the nice QCAD-man programmed the maths so you just choose one of the views and manually use it to develop an isometric drawing by copying and adding lines. And then deleting any lines that should be hidden behind the object. Although QCAD does most of the maths and sorts out the ellipses etc, it's still hard work converting 2D into isometric:

In 3D CAD, much better:  the object is modelled and because the shape is fully defined in 3 dimensions, the computer can do everything needed, almost effortlessly. The object can be rendered as 2D drawings, with sections, or in isometric, perspective, and photo-realistic views from any angle.

Isometric maths is really making my head hurt and I don't see why everyone else shouldn't suffer too!  Watch this space…

Dave

Edited By SillyOldDuffer on 11/04/2019 15:05:14

[Neil WyattModerator @neilwyatt]

Do it the old fashioned way!

Get a set of French curves and choose the best fit by eye.

[Ivan GinatoParticipant @ivanginato28142]

Posted by SillyOldDuffer on 11/04/2019 15:01:29:

Ivan's problem highlights the advantage of 3D CAD over pencil and paper methods and 2D CAD. For example, QCAD has basic tools that allows the draughtsman to nudge shapes into isometric form.

The isometric lines are created by transforming and rotating the drawing. Might have a go at explaining the maths but the number-crunching is quite involved.

Anyway, the nice QCAD-man programmed the maths so you just choose one of the views and manually use it to develop an isometric drawing by copying and adding lines. And then deleting any lines that should be hidden behind the object. Although QCAD does most of the maths and sorts out the ellipses etc, it's still hard work converting 2D into isometric:

In 3D CAD, much better: the object is modelled and because the shape is fully defined in 3 dimensions, the computer can do everything needed, almost effortlessly. The object can be rendered as 2D drawings, with sections, or in isometric, perspective, and photo-realistic views from any angle.

Isometric maths is really making my head hurt and I don't see why everyone else shouldn't suffer too! Watch this space…

Dave

Edited By SillyOldDuffer on 11/04/2019 15:05:14

Actually, I draw with paper and pencil as a hobbie. I've been studying AutoCAD and SolidWorks too. My teacher said me the paper and pencil method improve my horizon of imagination.

[Ivan GinatoParticipant @ivanginato28142]

Posted by Perko7 on 11/04/2019 09:31:10:

When I did my tech drawing training back in 1970, we were taught to draw it out in plan and elevation first, then draw construction lines at regular intervals perpendicular to the long axis which intersect the arcs. Then we could measure the offset and repeat that for drawing isometric or oblique views. The curve then became a freehand 'join the dot's as it rarely was a constant radius. Hope this helps.

Either by i've never seen it before or by not being anglophone I can't understand this method. Actually I think it is like a development surface methods? Like the following image:

Development surfaces

 

Edited By Ivan Ginato on 11/04/2019 17:13:46

Edited By Ivan Ginato on 11/04/2019 17:16:01

[JasonBModerator @jasonb]

It is a bit surface development, I illustrated the method earlier with this quick sketch

On the plan you draw a set of evenly spaced lines at right angles to one axis. Then on the Isometric draw the two axis with a 60/30degree set square and also use that to repeat the set of lines. You can then either measure the length of these lines on the plan view and mark the same lengths off on the isometric or use dividers to pick up the lengths and transfer to the isometric. Finally freehand join all the marks on the lines into a nice flowing curve.

If you want to see it done with more accuracy than the sketch just ask and I will dust of my drawing board.

Edited By JasonB on 11/04/2019 17:19:57

[Perko7Participant @perko7]

Yes Ivan and JasonB, it is surface development like you have stated, I just couldn't remember the correct terminology.

Neil, I well remember the French Curves we used to use, never could get an exact fit but usually got close enough with a little angling of the pencil where necessary.

Instead of free-handing, we used to use a flexible rule which was a rubbery/plastic 1cm square rod about 40cm long with a soft metal wire of some kind through the core. When you set it to a curve it would just stay there until you straightened it.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by SillyOldDuffer on 11/04/2019 15:01:29:

The isometric lines are created by transforming and rotating the drawing. Might have a go at explaining the maths but the number-crunching is quite involved.

.

I will be interested to see your explanation, Dave

MichaelG.

.

Sorry; I probably can't contribute for a few days, but it's something that I worked-out how to do in Autocad [early DOS version] more than 30 years ago … in just a few simple steps.

[SillyOldDufferModerator @sillyoldduffer]

Posted by Ivan Ginato on 11/04/2019 16:54:55:

Posted by SillyOldDuffer on 11/04/2019 15:01:29:

Ivan's problem highlights the advantage of 3D CAD over pencil and paper methods and 2D CAD.

…

Dave

Actually, I draw with paper and pencil as a hobbie. I've been studying AutoCAD and SolidWorks too. My teacher said me the paper and pencil method improve my horizon of imagination.

No criticism intended Ivan, my fault – I drifted onto CAD. I use paper and pencil too. The techniques used before computers are interesting and useful. Well worth looking at hand methods, for example, I find CAD drawings lack character compared with hand-drawn draughtsmanship, which can be beautiful.

Dave

[CirclipParticipant @circlip]

"Instead of free-handing, we used to use a flexible rule which was a rubbery/plastic 1cm square rod about 40cm long with a soft metal wire of some kind through the core. When you set it to a curve it would just stay there until you straightened it."

"Flexicurve" , square Lead core with two stainless strips encased in a soft PVC moulded sleeve. Easy way to straighten it was to "Whip" it onto the desktop. Have a later type made from interlocking plastic channel sections, can't get a tight radius, just like the FC. but a piece of solder helped.

Regards Ian.

[Cornish JackParticipant @cornishjack]

Have had a 'Flexicurve' for many years and very useful too but was offered this, some years ago. It offers a reasonable variety.

Anyone care to hazard a guess as to its origin? Ex Weybridge chaps might be at an advantage!

rgds

Bill

[Ivan GinatoParticipant @ivanginato28142]

Posted by JasonB on 11/04/2019 17:15:47:

It is a bit surface development, I illustrated the method earlier with this quick sketch

On the plan you draw a set of evenly spaced lines at right angles to one axis. Then on the Isometric draw the two axis with a 60/30degree set square and also use that to repeat the set of lines. You can then either measure the length of these lines on the plan view and mark the same lengths off on the isometric or use dividers to pick up the lengths and transfer to the isometric. Finally freehand join all the marks on the lines into a nice flowing curve.

If you want to see it done with more accuracy than the sketch just ask and I will dust of my drawing board.

Edited By JasonB on 11/04/2019 17:19:57

I would not dare ask you to do it for me, but I would dare ask you some material, book, pdf etc about it. Actually at my school is not give importance to paper and pencil drawing then I am doing it by myself.

[JasonBModerator @jasonb]

Watch this

[Ivan GinatoParticipant @ivanginato28142]

Posted by JasonB on 12/04/2019 16:56:04:

Watch this

Ok. Really thanks, man!

[SillyOldDufferModerator @sillyoldduffer]

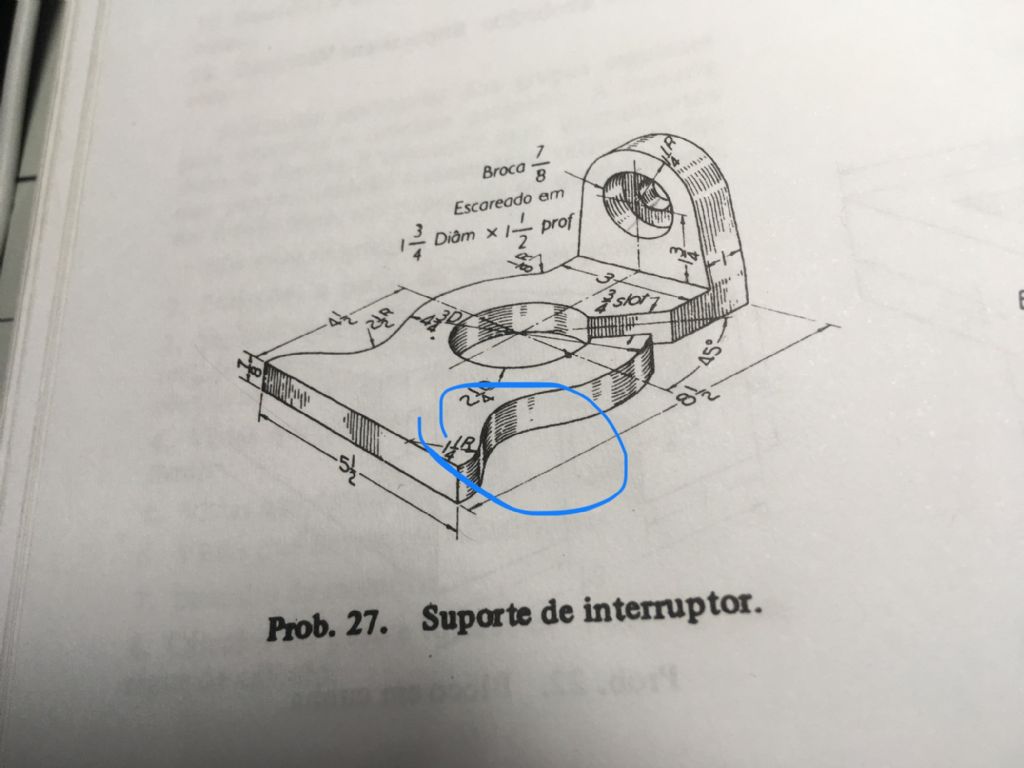
Slight diversion into the Oblique and Isometric Methods first.

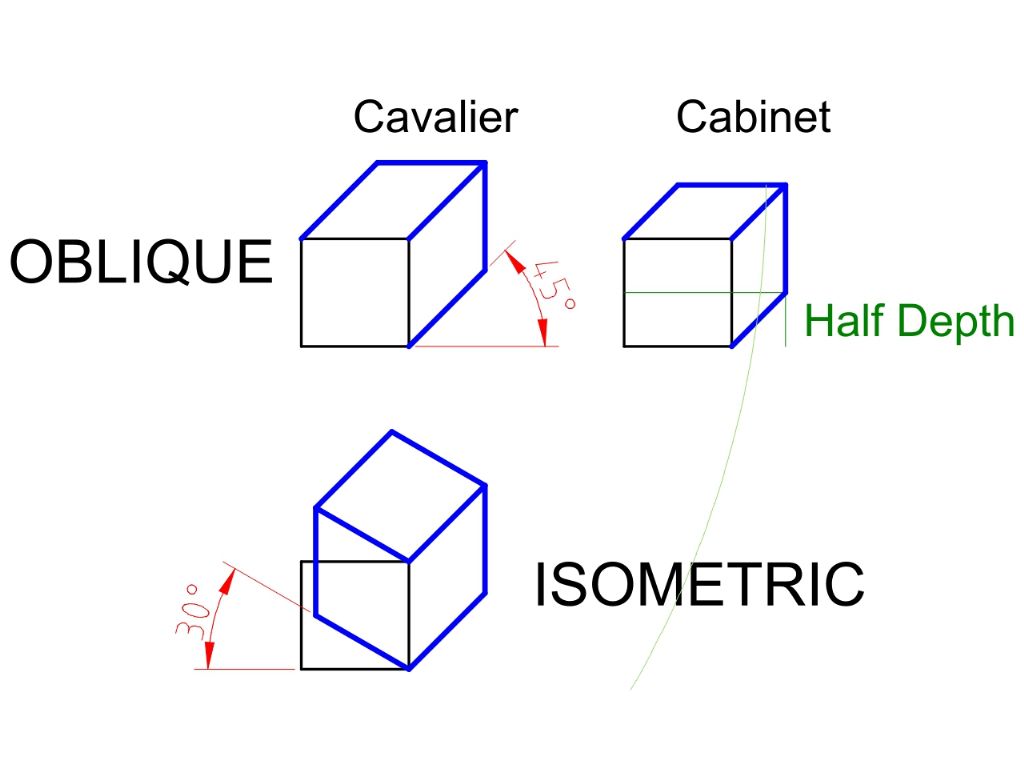
Oblique, presented at a 45° angle is easier to draw than isometric because the front face doesn't move. The Cavalier form retains the correct depth dimension and looks odd, Cabinet halves the depth as shown and looks more like a cube. Isometric is rotated at 30° and looks better.

Note that none of these projections are trustworthy in terms of dimensions or angles, which is why they are unwelcome in the workshop.

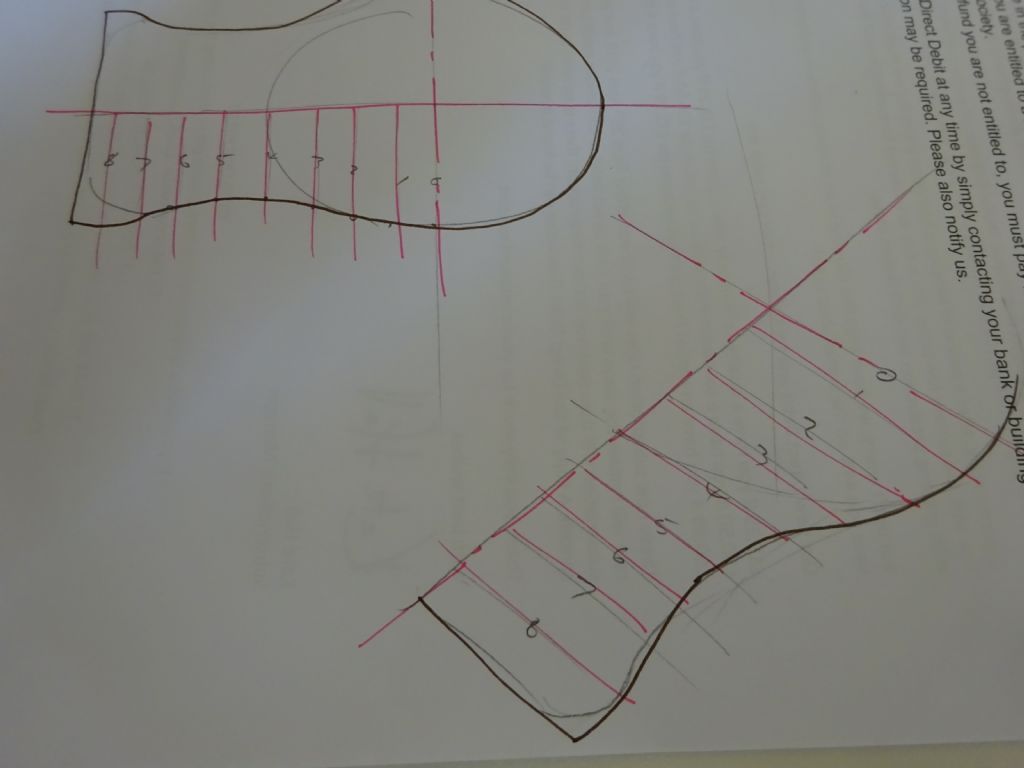
Similar to Jason's method, and as an introduction to how a computer might do an isometric projection:

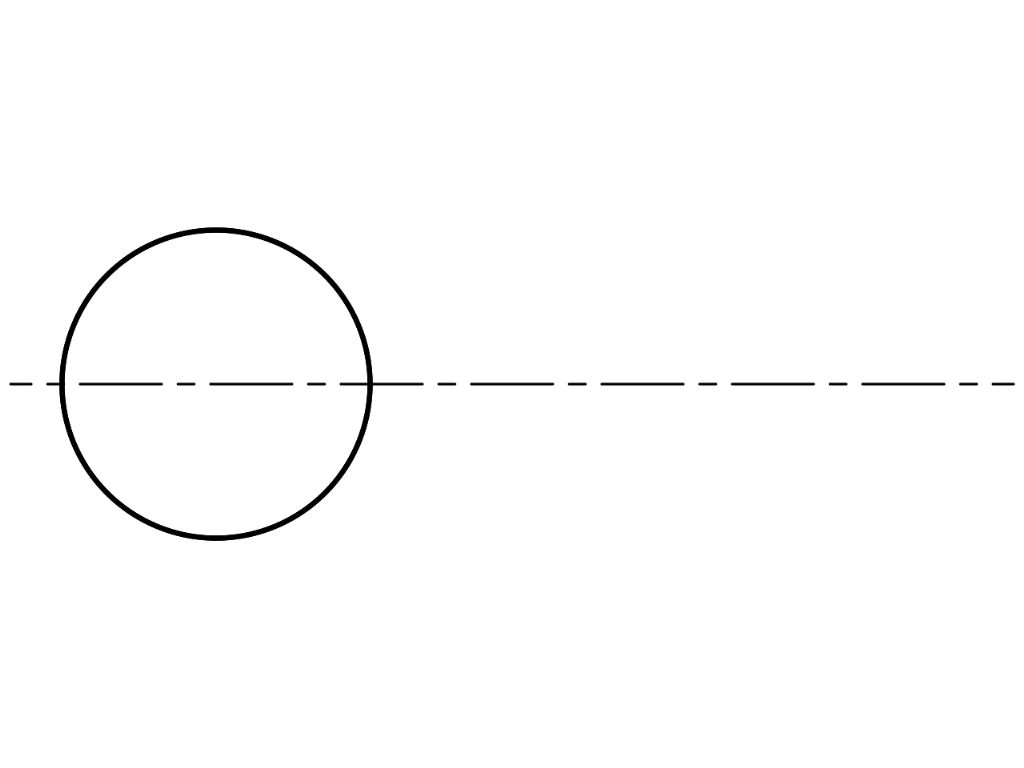
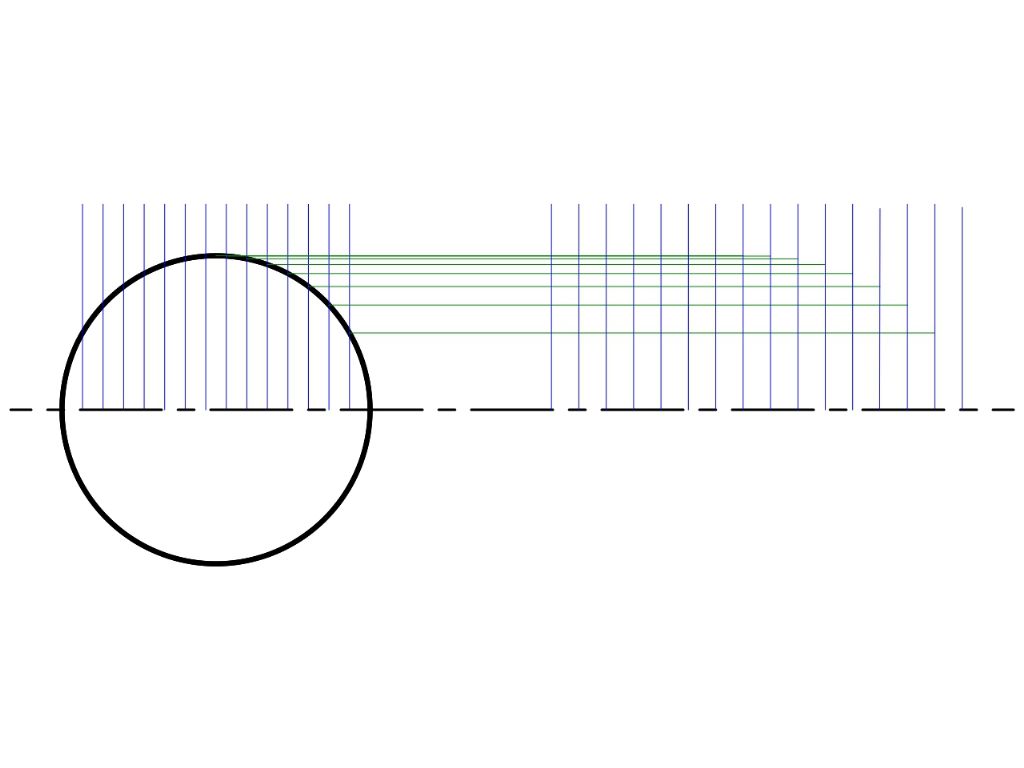
1. Draw a circle representing the end of a cylinder and, to show alignment, a centre line:

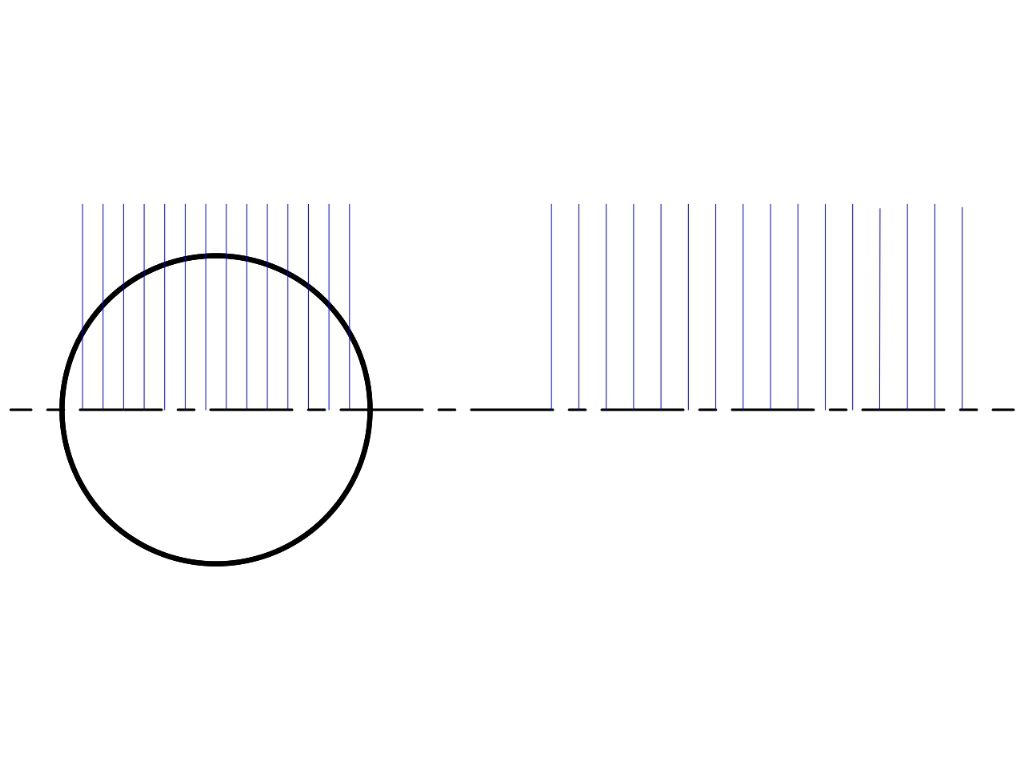
Next add two grids. Normally with the same separation, I've widened that on the right to emphasise the process – unnecessarily as it turned out. Doing this manually I used 15 grid lines, additional lines produce a more accurate ellipse but the process is a lot more work and pencil and paper limit the visible benefit. A computer has no such restrictions, the transformation can have as many points as wanted, which makes it possible to scale isometric drawings freely. 

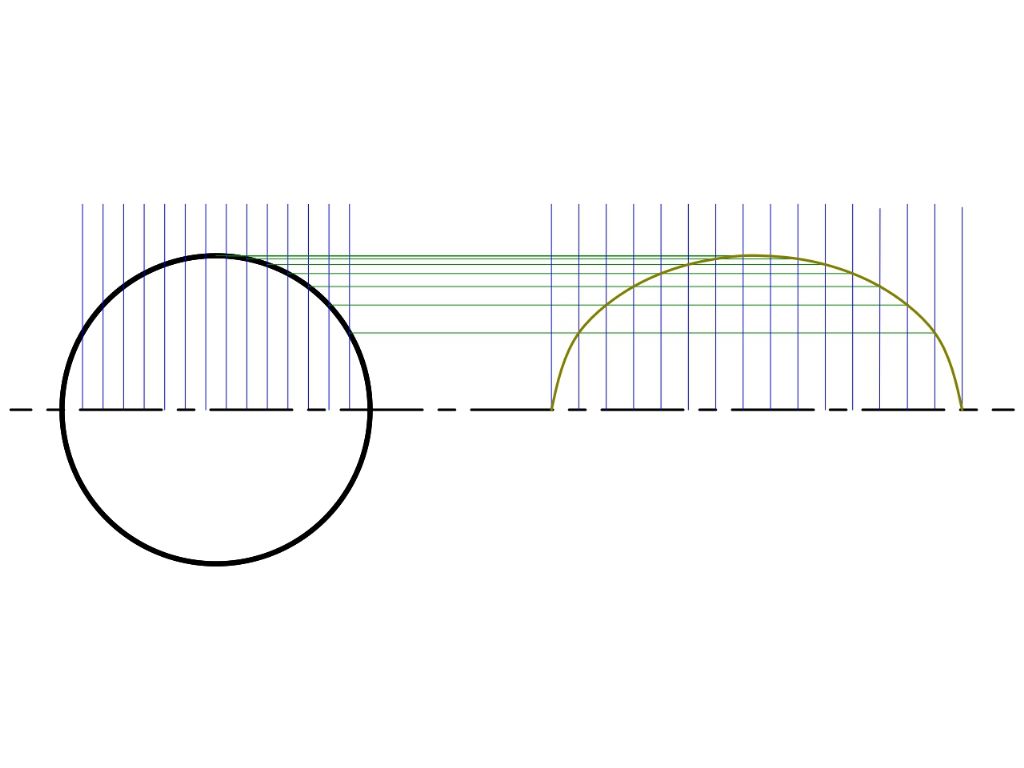
Add horizontals to map points from the circle to form an ellipse. This is a transformation, and it has the effect of producing new coordinates for the circle that make if appear to be turned sideways. Rather than drawing lines between grids on paper, transformations are done mathematically by the computer.

The ellipse is drawn by joining the new points.  All lines and shapes can be drawn by connecting points.

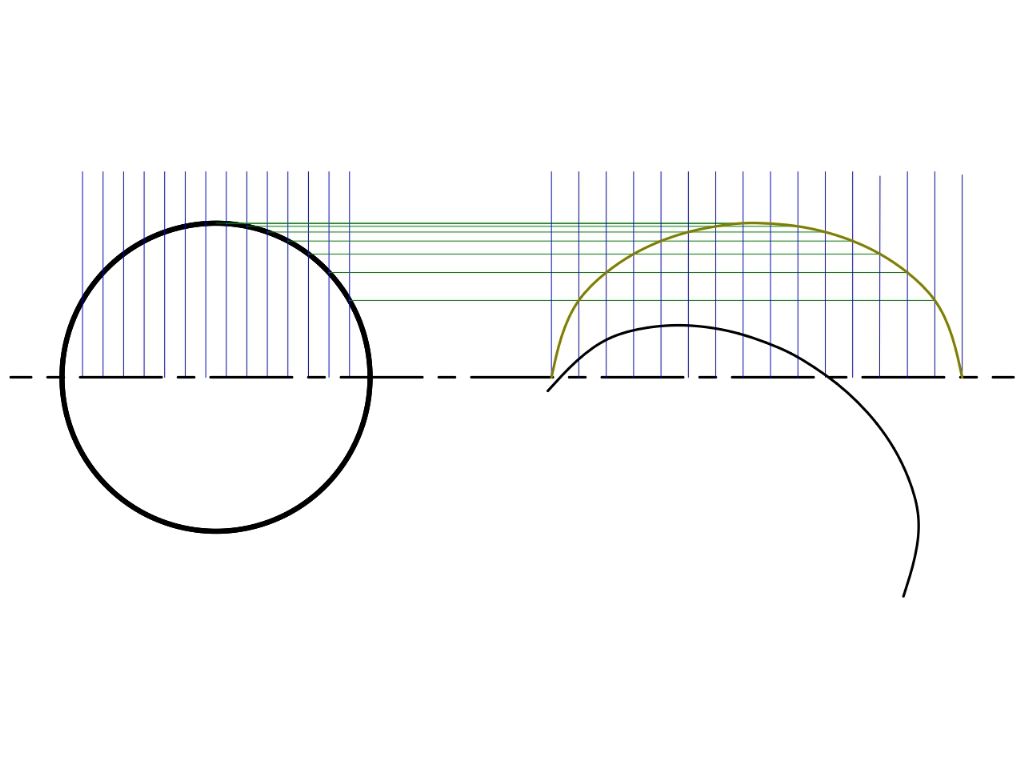
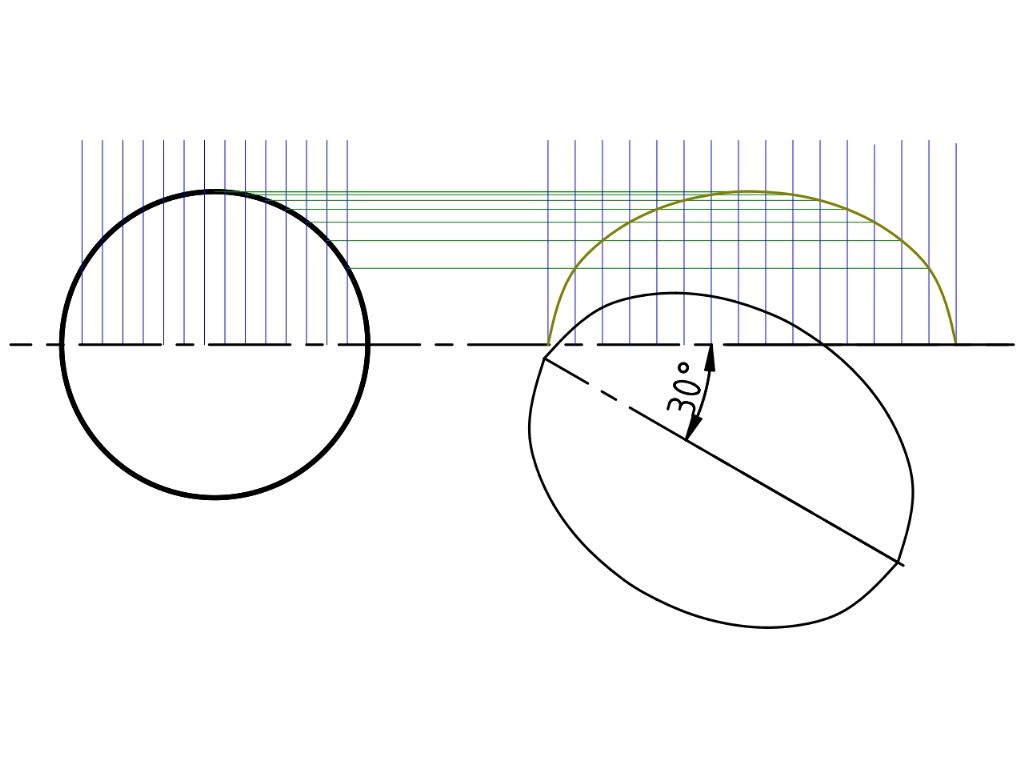
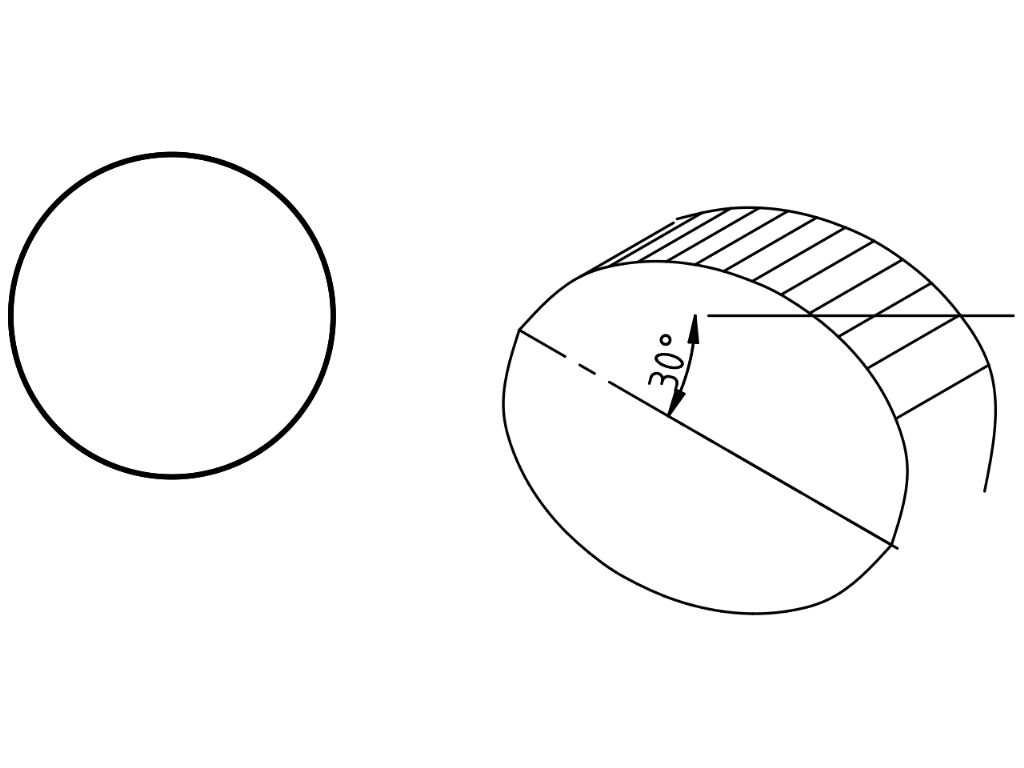
The ellipse is not yet in isometric form. It has to be rotated by 30°

 

The complete ellipse is produced by mirroring the top half, another numeric transformation:

Finally, the isometric depth is produced by replicating the top half of a the ellipse and moving it up and sideways:

All this can be done by manipulating the x,y coordinates of the lines, here's an outline of the maths:

In practice transformations are performed using matrices. Matrices allow moves and rotations to be combined together, and, surprisingly, the computer instructions are more efficient than solving the equations one after the other.

Even in this simplified overview it's obvious that a lot of calculations have to be done. So many that the method isn't really practical for people. Fortunately computers are really good at high-speed maths. Just as well, because the much same calculations with the addition of z coordinates, are used to translate 3D models into CNC tool paths. No way can a CNC machine follow a French Curve or guess – it has to told exactly where to go next . Bodging curves is not allowed!

This has been another exercise in self education for me. Delighted to have mistakes identified and corrected!

Dave

 

Edited By SillyOldDuffer on 12/04/2019 18:43:35

[Ivan GinatoParticipant @ivanginato28142]

Really nice, Silly. It’s always a pleasure take leassons like that.

[Author]

Posts