Antikythera Mechanism

[Michael GilliganParticipant @michaelgilligan61133]

Posted by drewt on 13/11/2021 02:50:06:

[…]

Attached is our Figure 2, a composite that is planar to the channel and decent (but not full) resolution.
[…]

.

Much appreciated, Drew !

May I suggest that anyone on the forum who is interested should now ‘have a go’ using that image and whatever technique they choose … Then, in a week or two, perhaps, we can share and compare our results.

MichaelG.

[John McNamaraParticipant @johnmcnamara74883]

Hi All

Thank you Drewt for the image, I am not exactly sure who to acknowledge regarding its copyright. However I wish to acknowledge that it is.

More testing and again differing results!
I have been using Autocad to work on the image, I did not select any centre points when placing the true circular arcs. I just used the three point arc method. I am confident the method is accurate.

To me the results all point to distortion.

How many holes? So far the tests have suggested a lower number certainly not 365 is the most likely?

Regards
John

[Michael GilliganParticipant @michaelgilligan61133]

I’m a big fan of three-point circle fitting, John … but your exercise raises a tricky question, to which I don’t currently have an answer.

It seems intuitively obvious that if the three points span a small angle, ‘confidence level’ must be lower than if they span a large angle … but what numbers can we put to that ?

MichaelG.

Edited By Michael Gilligan on 13/11/2021 12:26:36

[drewtParticipant @drewt]

Posted by John McNamara on 13/11/2021 08:20:52:

Hi All

Thank you Drewt for the image, I am not exactly sure who to acknowledge regarding its copyright. However I wish to acknowledge that it is.

More testing and again differing results!
I have been using Autocad to work on the image, I did not select any centre points when placing the true circular arcs. I just used the three point arc method. I am confident the method is accurate.

To me the results all point to distortion.

How many holes? So far the tests have suggested a lower number certainly not 365 is the most likely?

Regards
John

John,

Putting it this post is fine, I've added the copyright to the image metadata on this site. For anyone that wants to use it in an actual publication (print or electronic), you'd cite: "Budiselic, Chris, Andrew T. Thoeni, Michael Dubno, and Andrew T. Ramsey (2021), “Antikythera Mechanism: Evidence of a Lunar Calendar,” Horological Journal, 163 (3), 104–12."

On your point of measuring, I'd agree with your approach as the three point method effectively is using chords against extant physical features (the holes). As you note, large chords provide more accurate outcomes. However, you'll find variations of the outcome depending on which three holes you choose (since they are not all perfectly aligned to a circle). We ran into this problem and, instead of being susceptible to arguments we "cherry-picked" the data, we took advice from Dr. Dennis Duke, Department of Physics at Florida State University and calculated the center point for *every* possible combination of holes (there are 26,220 combinations). We used simultaneous equations for each of these combinations (thank you, computers) to find X and Y of the center and used the mean of all of these to determine the statistical center point (the mean and confidence intervals).

Best,

Drew

[Andre ROUSSEAUParticipant @andrerousseau66124]

A question that some may be in a position to answer:

Everyone would love to know the identity of the builder of the A.M. A few short years ago I read an online reference to some of the A.M.'s text translations which stated that it was "built by a Pythagorean"

I have never since come across an independent corroboration of this claim.

Can anyone categorically confirm or refute?

[Michael GilliganParticipant @michaelgilligan61133]

This may be the article that you have in mind, Andre : **LINK**

https://greekreporter.com/2021/03/13/antikythera-mechanism-the-worlds-first-computer-continues-to-amaze-scientists/

MichaelG.

.

Quote: “The most important thing is that we see laws of physics applying inside the mechanism, and the proof is in the inscriptions and the numbers 76, 19, and 223 that also show the name of the manufacturer, which tell us clearly ‘I am a Pythagorean,’” Moussas said.

Edit: __ Who he ? ___ https://youtu.be/kKuarnNBQyg

Edited By Michael Gilligan on 14/11/2021 08:24:35

Edited By Michael Gilligan on 14/11/2021 08:49:49

[Michael GilliganParticipant @michaelgilligan61133]

A couple of videos to refresh [and perhaps expand upon] our Pythagorean knowledge:

**LINK** : https://youtu.be/_PyPOXXPIJQ

**LINK** : https://youtu.be/p-0SOWbzUYI

MichaelG.

[John McNamaraParticipant @johnmcnamara74883]

Hi Drewt

I should have made it clear in the last post I made that all the arcs placed with the three point method were positioned on the end circle centres. The two "feature" arcs were positioned entirely by eye.

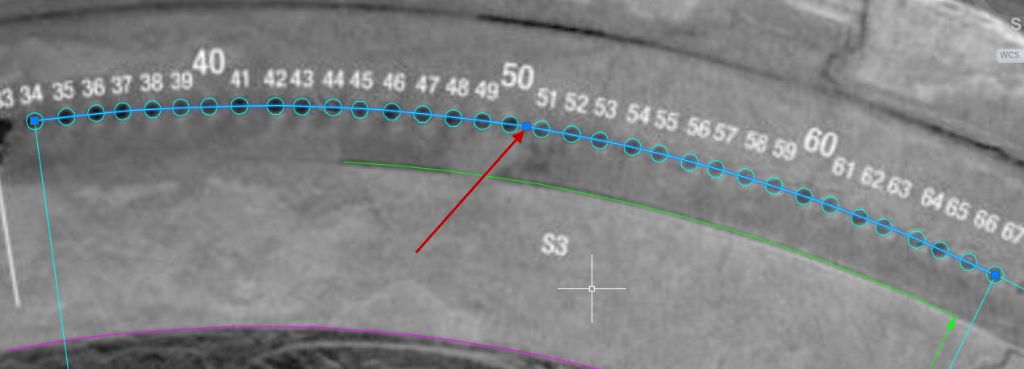
The centre of the hole(s) arc was positioned by eye as seen below. I tried to visually pick the visual average centre of all the holes.

The circles around the holes were also positioned by eye, prior to placing the arc. Reviewing the placement used it looks about right, Improving it would not significantly affect the placement of the arcs. and the the all important radius that assists us in calculating the number of holes.

I am surprised how much the the centres of the hole arcs and the two feature arcs deviate in the tests. There is significant error, they should line up better, assuming the creator had a half decent compass. It is clear the device was created by master craftsman. They would have had high quality compasses and tools.

For me that only leaves distortion, the centres should align a lot more accurately. was this distortion physical? The result of unknown forces over time? Or could it be possible that the X-ray scanning methods introduced error. I know the imaging was done in slices, were they truly planar to the mechanism? Could there be some form of spherical distortion of the scanning beam?

I would really like to know more about the scanning method. what was the accuracy and linearity obtained particularly over the entire area of the objects. The fine detail is good but that is not all we need.

See enlarged images below

Edited By John McNamara on 16/11/2021 13:42:14

Edited By John McNamara on 16/11/2021 13:43:29

[david bennett 8Participant @davidbennett8]

Distortion in a machined bronze ring is inevitable when it is broken. Anyone who has machined even a small ring knows that when sawn through, it closes up due to internal stresses. A slip fit becomes a tight friction fit ( a fact I use deliberately when making making slip-on machine dials ) The amount of distortion on a ring with this ones history may be considerable.

dave8

Edited By david bennett 8 on 16/11/2021 14:06:25

[David TocherParticipant @davidtocher94033]

Surely the radii for each of the arc segments should be the same? John McNamara has values ranging from 268mm to 329mm. If they are that different because of distortion of the segments (resulting from the fractures) then I suspect no meaningful answer to the number of holes on the complete wheel is possible.

I wouldn't expect the centres of the arcs for each segment to be the same because of the fractures.

We are redoing the least squares fit of holes in a segment for the three largest sectors with the additional constraint that the radii be the same for the sectors. I'll report our results.

[drewtParticipant @drewt]

John,

I am certainly no expert on the imaging techniques that were used. But, to my understanding, the images were done by rotating the object in a field, there slices are rendered, not a natural artifact of the imaging. There are some places where errors are present in the image data, but since it's data, you get, essentially, blank areas (or obvious distortion) where the rendering software can't calculate an outcome. Overall, Andrew Ramsey communicated to me that, for our purposes, we have X, Y, and Z rendered at 0.05 mm, the resolution of the original scans.

I would agree that, especially fitting an arc, that obvious misalignment occurs. However, I am pretty sure (going on my recollection here) that all of these were explainable by measured "distortion" due to cracks in the plate. While I agree with David that internal stresses are released when one machines a part, the maker would likely have wanted a slip fit of the calendar ring and the channel and since these would have been "machined" by hand—a slow process that provides feedback—, the effects fo the stress release would be noticed and the maker would continue to cut the channel (or file the ring) to obtain the desired fit.

[drewtParticipant @drewt]

David,

Yes, one would presume the radii would all be the same (if they were all part of a single circle, which no one thinks otherwise). Anyone attempting to mark off arcs should constrain them to within the sections noted in the image I provided (and described in the paper). Even then, some of the sections are so small, the error of marking an arc (or chord) grows. And, of course, the errors present in the work has an outsized effect if the arc is short.

[david bennett 8Participant @davidbennett8]

Drewt, the point I was trying to make is on the stress-relief distortion after the ring was broken, not during manufacture.

dave8

[Michael GilliganParticipant @michaelgilligan61133]

Just a thought …

Whilst we are all happily enlarging these images for convenient viewing and measurement … let’s take a moment to contemplate the scale of the device.

I have previously tabulated some numbers … but this evening I was playing with QCAD : drew the circle of holes and printed them life-size.

It’s a useful reality-check.

MichaelG.

Edited By Michael Gilligan on 16/11/2021 23:37:50

[SillyOldDufferModerator @sillyoldduffer]

This Smiths Timer reminded me of the Antikythera ring:

A pin in the lower ring flips a microswitch on, while a pin in the outer ring flips it off. 96 holes divide a 24 hour cycle into 15 minute segments. Much less challenging to make the ring than that on the Antikythera device. Setting the timer is a little fiddly, and I think the holes are about as close as they can be for ordinary fat fingered folk.

Struck me the Smiths pins have two separate functions: they drive a switch and they indicate the time. Possibly the Antikythera does similar. I think the Antikythera pins are too small and weak to drive gears or move the ring. Therefore I suggest the holes are intended to hold indicator pins. A pin might be inserted to indicate 'new moon today', after which cranking the device would move the ring and pin to show the dates on which future new moons occur. This movement might be relative to the Egyptian Civil Calender marked on the dial, and maybe one of the mechanism's functions is to convert lunar time into solar. For example: If tonight is the second new moon of the year in Athens (Lunar), how many days are there until the 23rd of Renwet in Thebes (Solar)?

Dave

[david bennett 8Participant @davidbennett8]

Dave, interesting idea, but isn't it thought that the ring of holes is covered by a caledar dial of some sort? I was toying with the idea that a relatively simple mechanism might have existed showing any useful various calendars/moon phases etc. on one dial with different hands as indicators (maybe incorporated in the AM or a stand-alone instrument)

dave8

Edited By david bennett 8 on 19/11/2021 15:56:09

[Dave HalfordParticipant @davehalford22513]

Has anyone on here ever drawn bronze wire down to 0.3mm if so how strong was it?

[egaParticipant @ega]

SOD:

Isn't the time on the Smiths timer witnessed by the notch at the 12 o'clock position?

[david bennett 8Participant @davidbennett8]

Posted by SillyOldDuffer on 19/11/2021 15:32:03:

This Smiths Timer reminded me of the Antikythera ring:

A pin in the lower ring flips a microswitch on, while a pin in the outer ring flips it off. 96 holes divide a 24 hour cycle into 15 minute segments. Much less challenging to make the ring than that on the Antikythera device. Setting the timer is a little fiddly, and I think the holes are about as close as they can be for ordinary fat fingered folk.

Struck me the Smiths pins have two separate functions: they drive a switch and they indicate the time. Possibly the Antikythera does similar. I think the Antikythera pins are too small and weak to drive gears or move the ring. Therefore I suggest the holes are intended to hold indicator pins. A pin might be inserted to indicate 'new moon today', after which cranking the device would move the ring and pin to show the dates on which future new moons occur. This movement might be relative to the Egyptian Civil Calender marked on the dial, and maybe one of the mechanism's functions is to convert lunar time into solar. For example: If tonight is the second new moon of the year in Athens (Lunar), how many days are there until the 23rd of Renwet in Thebes (Solar)?

Dave

Dave, there seems to be a misunderstanding of the Mechanism (which made me think I was missing something) As I understand it, none of the dials or hole rings move when the thing is cranked. All that happens is that the related "pointers"move – except the calendar dial is manually moveable for adjustment.

dave8

Edited By david bennett 8 on 20/11/2021 00:16:46

Edited By david bennett 8 on 20/11/2021 00:18:21

[david bennett 8Participant @davidbennett8]

Posted by Michael Gilligan on 12/11/2021 08:31:48:

Posted by david bennett 8 on 12/11/2021 01:34:38:

.

 

We now know the actual solar year is 365.24 days. Over 4 years the error would be 0.96 days.

.

Alternatively; using Hipparchus’s figure, it would be 0.98668

… pick a number !

MichaelG.

I did pick a number – I chose todays results to compare with the AM designers figures . (I know this is a late reply, but I have just been re-reading the posts)

dave8

 

Edited By david bennett 8 on 21/11/2021 02:19:54

Edited By david bennett 8 on 21/11/2021 02:22:48

[Michael GilliganParticipant @michaelgilligan61133]

Posted by david bennett 8 on 21/11/2021 02:18:59:

Posted by Michael Gilligan on 12/11/2021 08:31:48:

Posted by david bennett 8 on 12/11/2021 01:34:38:

.

 

We now know the actual solar year is 365.24 days. Over 4 years the error would be 0.96 days.

.

Alternatively; using Hipparchus’s figure, it would be 0.98668

… pick a number !

MichaelG.

I did pick a number – I chose todays results to compare with the AM designers figures . (I know this is a late reply, but I have just been re-reading the posts)

dave8

.

Sorry, Dave … I honestly don’t understand the logic of your choice.

[ mostly because you started with a false premise ]

MichaelG.

.

P.S. __ If you really want to labour this [which I do not think is really appropriate] … you might find this interesting : 

https://www.hermetic.ch/cal_stud/cassidy/err_trop.htm

Edited By Michael Gilligan on 21/11/2021 07:57:22

[david bennett 8Participant @davidbennett8]

Michael G, I also do not wish to labour the point, but I would be interested ro know my false premise, and I doubt the extra decimal points would be relevant to a mechanism like this .

dave8

[Michael GilliganParticipant @michaelgilligan61133]

Posted by david bennett 8 on 21/11/2021 15:02:35:

Michael G, I also do not wish to labour the point, but I would be interested ro know my false premise, and I doubt the extra decimal points would be relevant to a mechanism like this .

dave8

.

O.K. Dave

You clearly stated, with [it appeared] some confidence:

"We now know the actual solar year is 365.24 days. Over 4 years the error would be 0.96 days."

… but that is, in fact, quite contrary to what "we now know"

What we do know is that the solar year varies from place to place and from time to time.

That's what I was hinting-at when I wrote:

"… pick a number"

.

I do agree that additional decimal places are likely irrelevant to the construction of the mechanism … but if we were to use anything for 'reverse engineering' , then Hipparchus’s figure would be near-contemporaneous and [rounded to two decimals] gives 0.99 rather than 0.96

MichaelG.

[david bennett 8Participant @davidbennett8]

Michael, thanks for your views. Finally, what in your opnion is the purpose of the ring of holes?

dave8

[Michael GilliganParticipant @michaelgilligan61133]

Posted by david bennett 8 on 21/11/2021 20:16:48:

Michael, thanks for your views. Finally, what in your opnion is the purpose of the ring of holes?

dave8

.

Until we can be more confident of the number of holes in the full circle, I am content to remain agnostic

MichaelG.

.

Ref. __ https://www.merriam-webster.com/dictionary/agnostic

Edited By Michael Gilligan on 21/11/2021 20:28:47

[Author]

Posts