Antikythera Mechanism
Antikythera Mechanism
Home › Forums › General Questions › Antikythera Mechanism
- This topic has 211 replies, 40 voices, and was last updated 17 November 2024 at 01:44 by
david bennett 8.
-
AuthorPosts
-
6 November 2021 at 15:24 #570160
david bennett 8
Participant@davidbennett8Posted by david bennett 8 on 06/11/2021 02:34:39:P.S — see also post by pgk pgk 07/10/21 12:10:45 He beat me to it.
dave8
Edited By david bennett 8 on 06/11/2021 02:37:34
Michael, I have just re-read the BHI papers you linked, and it reaffirms my doubts. It seems to assume the calendar dial is moved manually, daily,to the next hole in the plate behind it. This seems at odds with an instrument which uses a " pointer for referencing markings " If such a pointer was used (on one of the most important dials) then the holes would surely be for fine adjustments and irrelevant to the calendar divisions.
dave8
6 November 2021 at 15:24 #570161david bennett 8
Participant@davidbennett8Posted by david bennett 8 on 06/11/2021 02:34:39:P.S — see also post by pgk pgk 07/10/21 12:10:45 He beat me to it.
dave8
Edited By david bennett 8 on 06/11/2021 02:37:34
Michael, I have just re-read the BHI papers you linked, and it reaffirms my doubts. It seems to assume the calendar dial is moved manually, daily,to the next hole in the plate behind it. This seems at odds with an instrument which uses a " pointer for referencing markings " If such a pointer was used (on one of the most important dials) then the holes would surely be for fine adjustments and irrelevant to the calendar divisions.
dave8
6 November 2021 at 21:25 #570217 Michael GilliganParticipant@michaelgilligan61133Posted by david bennett 8 on 06/11/2021 15:24:02:
Michael GilliganParticipant@michaelgilligan61133Posted by david bennett 8 on 06/11/2021 15:24:02:
[…]Michael, I have just re-read the BHI papers you linked, and it reaffirms my doubts. […]
.
Wow, David !
There was I … only arrogantly believing that I might have found a better way of estimating the angles between the holes.
You appear to be dubious about the very concept.
MichaelG.
7 November 2021 at 18:57 #570341david bennett 8
Participant@davidbennett8Michael, yes. (no small thing to do, as there are many experts examining the mechanism) but I cannot find any reason for their conclusions on this matter apart from – because the holes are there they must be for something. ( not a quote) Thats why I thought I had missed something.
dave8.
7 November 2021 at 23:02 #570371david bennett 8
Participant@davidbennett8P.S. too late to edit above, but I note in part 2 of the BHI link that they propose a geared day pointer for the calendar ring ( which was manually moved in the first place! ) They seem to have come full circle to justify their conjecture which they say has no extant feature to confirm setting the calendar by the ring of holes.
dave8
Edited By david bennett 8 on 07/11/2021 23:02:40
Edited By david bennett 8 on 07/11/2021 23:04:39
9 November 2021 at 14:58 #570586John McNamara
Participant@johnmcnamara74883Hi All
Yes I am still around double Vaxed and healthy! I must however admit I will be happy to see the end of 2021.
Thought I would have a think on the problem and try to resolve it with CAD.
These are my findings, also in my Album.Somewhere between 360 and 366 segments
Maybe this could be refined a little but with a distorted part it would still be a guess.I hope I got the calculations correct.
9 November 2021 at 16:40 #570605 Michael GilliganParticipant@michaelgilligan61133
Michael GilliganParticipant@michaelgilligan61133Good to see you around here again, John
Your results differ greatly from mine; but I think this only goes to prove how difficult [near impossible] this exercise really is. … ‘non-trivial’ doesn’t even begin to describe it.
MichaelG.
10 November 2021 at 03:58 #570665John McNamara
Participant@johnmcnamara7488312 November 2021 at 01:34 #570916david bennett 8
Participant@davidbennett8I am becoming more convinced that the earlier BHI thoughts on the calendar dial ( pre the lunar dial suggestion) were correct . The 354 ? hole count would make a leap year correction more exact than a 365 hole count. We now know the actual solar year is 365.24 days. Over 4 years the error would be 0.96 days. A 354:365 day ratio would be 0.97 days. This would obviously be much more accurate than a 365 hole count for leap year corrections. This would allow reverting to the original idea of a gear driven pointer to indicate solar days.
dave8
Edited By david bennett 8 on 12/11/2021 01:41:57
Edited By david bennett 8 on 12/11/2021 01:47:40
12 November 2021 at 02:24 #570917david bennett 8
Participant@davidbennett8PS. A 351 hole count would be even closer.
dave8
Edited By david bennett 8 on 12/11/2021 02:24:53
Edited By david bennett 8 on 12/11/2021 02:43:10
12 November 2021 at 08:31 #570926 Michael GilliganParticipant@michaelgilligan61133Posted by david bennett 8 on 12/11/2021 01:34:38:.We now know the actual solar year is 365.24 days. Over 4 years the error would be 0.96 days.
Michael GilliganParticipant@michaelgilligan61133Posted by david bennett 8 on 12/11/2021 01:34:38:.We now know the actual solar year is 365.24 days. Over 4 years the error would be 0.96 days..
Alternatively; using Hipparchus’s figure, it would be 0.98668
… pick a number !
MichaelG.
12 November 2021 at 11:42 #570956 Neil WyattModerator@neilwyatt
Neil WyattModerator@neilwyattIt's been surmised that the device was more of a teaching aid than a precise calculator.
Neil
12 November 2021 at 13:09 #570976david bennett 8
Participant@davidbennett8Either way, the numbers support a solar calender and take away from a lunar one.
dave8
12 November 2021 at 14:32 #570991drewt
Participant@drewtPart 1
Hello (and G'Day),
I am the second author on the BHI article(s), responsible for data gathering and analysis in the article. Chris (first author) and I have been reviewing this thread with great interest. We have always wanted others to dig depper and review our work in earnest and try to extend it. We are happy to see that is happening here. I'd like to make a few small corrections, add a little context, and provide additional background not reported in the paper (editors don't like you to ramble on, but here&hellip
 . For clarity, the authors look at this as one article but BHI, wisely, split it into two, one about the finding, and the second about the implications. I will refer to it all as one article.
. For clarity, the authors look at this as one article but BHI, wisely, split it into two, one about the finding, and the second about the implications. I will refer to it all as one article.First, all credit to the initial observation of the calendar possibly not being 365 days and, importantly, the impetus to dig into this problem goes to Chris. A couple of scholars, notably Derek de Solla Price (1974), suggested the markings seemed inconsistent with 365 days, but then dropped the notion and never completed an assessment of the actual Mechanism. Since its discovery around 1900, nearly all scholars, and certainly current scholars, have assumed the calendar was 365-days. Some confronted with the Mechanism's calendar anomalies have, in our current view, struggled mightily to justify 365 days. This is a common human phenomenon called confirmation bias. We still hold open the possibility we suffer from the same bias, but thus far, the data suggests otherwise. With Chris's insight we set out to test if the calendar was based on 365 days.
Which leads to an important clarification in this thread. We took great pains to test the null hypothesis of "the number of holes underlying the Calendar ring is 365," making the alternative hypothesis "the number of holes underlying the Calendar ring is *not* 365." We do discuss in the paper what is likely (somewhere between 354 and 359, possibly 360 if you stretch significance), but our only true evidentiary finding is that the calendar is *not* 365 days. Of the frequently used calendar systems 354, 360, etc., and given the context and functions of the device, we *suggest* there is evidence of 354/lunar calendar, but we leave it to others to carry forward this analysis as we believe (and has been pointed out here) there is insufficient evidence to conclude it is 354. However, there is sufficient evidence to conclude it is *not* 365. See implications, below. We'd love nothing more than for another Mechanism to be found.
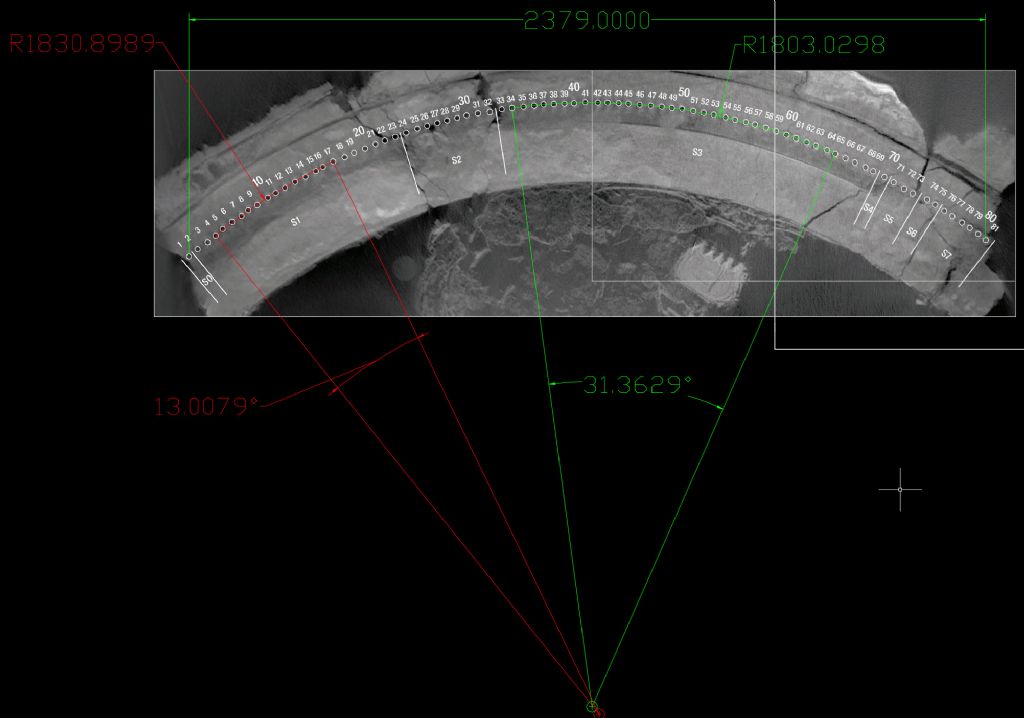
IMAGE. The image mostly being used in this thread is of poor quality and suffers from being a composite (as some have noted), being low print resolution, and not accounting for parallax error. The original scans were high-resolution (0.05 mm) X-ray computed tomography (CT) imaging and performed in 2005. I note an assumption in the thread that there must be better images of the Mechanism by now, but there are not. The AMRP and the National Archaeological Museum are, understandably, very protective of the Mechanism's fragile remains. In fact, when the images were made in 2005, the CT machines (quite large) had to be shipped to the Mechanism rather than vice versa.
The CT scans are a set of data points in three dimensions so need to be rendered. When rendering, one can select the plane of view and get a stack of images representing the Z axis for that rendering. Each image in the stack, therefore, has an X and Y axis. We were very fortunate to obtain two sets of renderings from our co-author, Andrew Ramsey, who personally lead the imaging portion in 2005 and captured the original data. (Interestingly, after 2,000 years, Andrew was the first person to see the ephemera engravings in the images of the Mechanism.) Our first set of renderings (about 1900 image layers, about 18 GB) was used to measure the plane of the channel in which the holes are drilled. From this we gave Andrew the specific plane to render to align the channel to the viewing plane, thus minimizing parallax error. Without Andrew's guidance and assistance, we could have not achieved a level of accuracy sufficient to draw a statistical conclusion.
I see a more recent post using our image but I'd again caution against that as though it is planar, it is a lower-resolution publishable version and a composite. You'll get closer measurements to ours than using the other image, but not close enough to, in my view, warrant the time. Our data are freely available and can save you a lot of time. =
12 November 2021 at 14:32 #570992drewt
Participant@drewtPart 2
MEASUREMENT. We experimented and tested multiple raw measurement methods for reliability, including all described in this thread. We found, by far, the most reliable method was locating the hole center. Even with our custom images, and ability to move up and down through the hole, measurement of a few holes is difficult due to being filled with silt. We note there are several fractures (which we identified by measuring Z-height of the channel and linerally using X-Y coordinates of matching features across fractures). A couple of the fractures are obvious, but we published some in the article others have not had the ability to detect. Accounting for fractures is particularly problematic in a composite image.
Our summary X,Y data are published and freely available at the Harvard dataverse (https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/VJGLVS). It took nearly a year of data gathering, analysis, correcting, re-imaging, data collecting again and again, to get the dataset we published. Therefore, we'd encourage people to use the published data or, if one is concerned about our data collection (we are happy to entertain critiques) plan on months of data gathering and assessment to get a "clean" dataset. I only mention this to save everyone time from attempting to measure the composite image. That method will be fraught with errors and only lead to frustration (ask me how I know).
Separately, I note David Toucher's Bayesian analysis of our published data where his conclusions are pretty close to what is shown in our Figure 3. Again, reminding that our hypothesis was determining only if the calendar is 365. David concludes there is a 1.5% posterior probability of 365 days but a 25.7% probability of 354 and 30% for 355. Also, I'll note we used multiple methods to check our results, including least squares and replicating all other methods/calculations previously published. All supported our finding (not 365).
IMPLICATIONS. Several people have asked, "so what?" Here I'll convey Chris's views (who is much more versed on this). The Mechanism's calendar has three visible Egyptian month names—the Egyptian civil calendar is known to have been 365 days. If the calendar is not 365 days, then we now have a puzzle. Why Egyptian month names on a Greek device, especially when the day count doesn't match the Egyptian civil calendar? Because this device appears to have been made in the northeastern Mediterranean (far from Egypt) but does not have 365 days, there are many clues here that our understanding of the Egyptian calendar systems (they had several), the purpose of the device, and the ongoing puzzle of the features and some gearing for those features are unresolved. In addition, the calendar not being 365 calls into question every model described and built thus far. As Chris described in the second part of the article, there are additional features of the Mechanism affected by 365/not 365 days.
QUESTIONS. This thread started with the valid question from Mike Edmunds about what kind of accuracy is possible/likely. I think this is an intersting question and one Chris and I have discussed at length. We are both amateur machinists (I a clockmaker and Chris a clockmaker and astoundingly skilled machinist and thinker) and based on research, Chris has a good understanding of the methods available when the Mechanism was constructed and also an understanding of what might be possible for an inventive maker like the one who designed the Mechanism. In this area, Chris's experimental work may be useful to you.
For the dividing plate (rod) proposal: https://youtu.be/BIUAdINXZmQ
Pump drill: https://youtu.be/OtWVA7_9Rik
Drill bit: https://youtu.be/N1aj_3tlQhUTo answer Mike's question I think it would be very helpful for someone to recreate the ring of holes with the published dimensions using the best effort and ancient tooling and methods, then accurately measure those results (with similar rigor as in the published article).
I am happy to address any other questions and explain our methods, etc. I'll check back on this thread in case any arise.
Best,
Drew
12 November 2021 at 17:21 #571034 Michael GilliganParticipant@michaelgilligan61133
Michael GilliganParticipant@michaelgilligan61133Great to have you aboard, Drew

MichaelG.
12 November 2021 at 18:04 #571043 Michael GilliganParticipant@michaelgilligan61133Posted by drewt on 12/11/2021 14:32:07:
Michael GilliganParticipant@michaelgilligan61133Posted by drewt on 12/11/2021 14:32:07:[…]
IMAGE. The image mostly being used in this thread is of poor quality and suffers from being a composite (as some have noted), being low print resolution, and not accounting for parallax error. The original scans were high-resolution (0.05 mm) X-ray computed tomography (CT) imaging and performed in 2005.
[…]
.
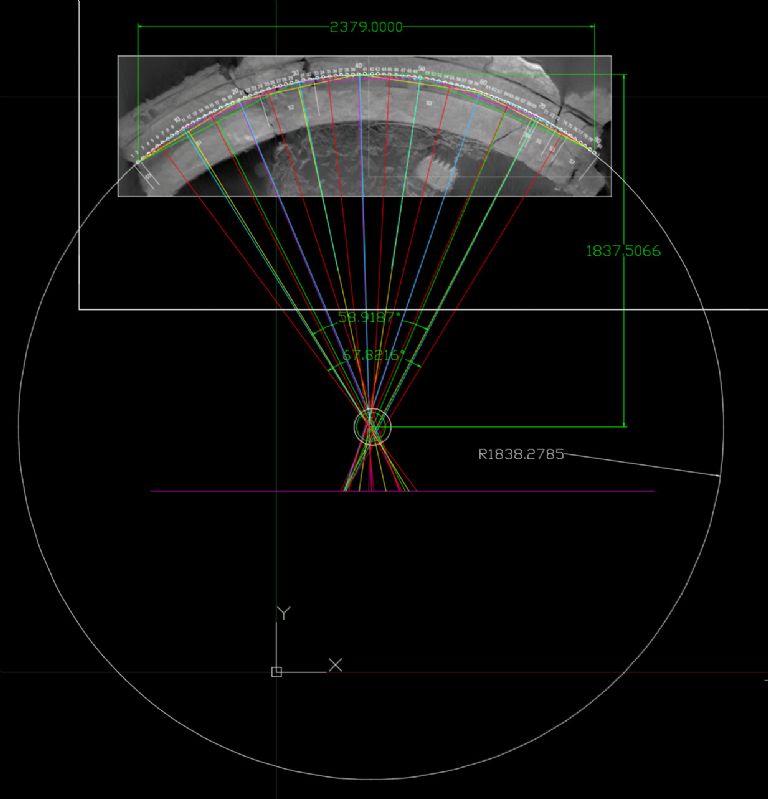
One observation on that, if I may, Drew
Admittedly, I was working with an inferior image for my own efforts … but I did express some concern that your team was using XY co-ordinates based on 0.05mm resolution.
Frankly, I do not think that it is possible to reliably extrapolate the number of holes in the full circle when you are using rectangular co-ordinates at that resolution.
Crude as it was … I believe that my technique of directly estimating the angles [using an up-scaled, resampled, image] might have the potential to produce a better result.
MichaelG.
12 November 2021 at 20:15 #571059drewt
Participant@drewtPosted by Michael Gilligan on 12/11/2021 18:04:15:Posted by drewt on 12/11/2021 14:32:07:[…]
IMAGE. The image mostly being used in this thread is of poor quality and suffers from being a composite (as some have noted), being low print resolution, and not accounting for parallax error. The original scans were high-resolution (0.05 mm) X-ray computed tomography (CT) imaging and performed in 2005.
[…]
.
One observation on that, if I may, Drew
Admittedly, I was working with an inferior image for my own efforts … but I did express some concern that your team was using XY co-ordinates based on 0.05mm resolution.
Frankly, I do not think that it is possible to reliably extrapolate the number of holes in the full circle when you are using rectangular co-ordinates at that resolution.
Crude as it was … I believe that my technique of directly estimating the angles [using an up-scaled, resampled, image] might have the potential to produce a better result.
MichaelG.
Michael,
I am very happy that people are questioning this work and methods. So, please do so.
Yes, we'd like higher resolution also. But, a couple of things are important about the question "is there enough resolution?" at least in my view. First, resolution helps more accurately define the edges, the specificity of the circle. Assuming the resolution is roughly the same around the circumference of a hole, the "errors" tend to average out. Not, of course, perfectly, but pretty reasonably below 0.05 mm, say somewhere between 0.025 and 0.035. Secondly, multiple measures of the same center points reduces this error by averaging the measures. I think this is noted in the paper, but we took multiple measures of the same hole (at different points in time to avoid our own bias) until we reached measurement saturation, that is, the X,Y center point became fixed within ≤ 0.05 standard deviation; we actually reached 0.037 mm. The value of statistics is it allows us to deal with these ambiguities by measuring errors and conveying a confidence and standard error value. While I agree higher resolution would be better, the resolution is very adequate for testing 365, but not adequate to confirm 354. This is evidenced by the fact we have a p-value for 354 of 0.005 and a p-value of 365 as 0.102 on the TOST procedure.
On the alternative measure of angles. We considered this early on and Chris, in fact, had done some work similar to what you have done. The problem is, to measure an angle you have to presume a center point. Since there is only a fraction of the circle available, and that is fractured, establishing a center is quite variable—so much so it would not reduce variability to a significant level. To also prevent others from suggesting we were cherry-picking the center point (which does not physically exist), our goal was to determine the center using only extant physical features. Once we'd concluded the center, we did go back and perform the same angle calculation you are doing and they line up surprisingly well at 354 days.
Finally, I think it may be important to define your term "better result." To me, that's a better standard error, higher confidence, lower variation caused by measurement error, etc. None of the authors really have a horse in the 365/360/354-day outcome, we just want the extant physical features to generate data we all can rely on to better understand the Mechanism.
Hope this helps. Again, feel free to disagree.

Drew
12 November 2021 at 21:49 #571069SillyOldDuffer
Moderator@sillyolddufferPosted by drewt on 12/11/2021 14:32:27:Part 2
…
The Mechanism's calendar has three visible Egyptian month names—the Egyptian civil calendar is known to have been 365 days. If the calendar is not 365 days, then we now have a puzzle. Why Egyptian month names on a Greek device, especially when the day count doesn't match the Egyptian civil calendar? Because this device appears to have been made in the northeastern Mediterranean (far from Egypt) but does not have 365 days, there are many clues here that our understanding of the Egyptian calendar systems (they had several), the purpose of the device, and the ongoing puzzle of the features and some gearing for those features are unresolved….
Many thanks for your posts and welcome to the forum Drew.
The Egyptian connection doesn't seem strange to me: although Egyptian civilisation predates ancient Greece, the two overlapped and the peoples must have been known to each other: probably plenty of trade and cultural exchange.
I support the hypothesis the holes are lunar because using the moon as a clock is considerably easier than the sun. Back then astronomers didn't have much instrumentation beyond the Mk 1 eyeball. No problem – the beginning of each lunar month is clearly marked by, for example, the first appearance of a crescent moon. The sun has no such clear time markers. Instead it's necessary to identify the days on which sun is highest and lowest in the sky, or measure accurately when day and night are equal. Quite difficult. I think early calendars were lunar for practical reasons – the moon is the most obvious clock in the sky, easy to see and count.
The main disadvantage of lunar calendars is the seasons drift because they depend on the sun, which isn't synchronised with the moon. Thus later calendars adjusted lunar months to align with seasons by adding extra days in a number of different ways.
Apart from Easter, which no-one understands,, we use nothing but solar time today. Perhaps that makes it's hard for us to accept lunar observations are the mother lode. If Wikipedia is to be believed all the states of ancient Greece used nothing but lunar calendars, and the Egyptian civil calendar was derived from their lunar calendar. It appears to be worldwide – everyone started with lunar observations.
Possibly the Antikythera device mechanised intercalation, perhaps generating the Egyptian Civil calendar from lunar observations. Fascinating stuff – I wish more of the mechanism had survived.
Dave
12 November 2021 at 21:49 #571070pgk pgk
Participant@pgkpgk17461I remain puzzled by what and how these holes could be used. Holes don't strike me as a useful gear mesh and ought to be more regular than these images suggest to work with tiny points on another gear. If all holes were converted to hold pins then presumably statistics imply some pins would remain unless made of a material that fully corroded. Could they be merely sighting holes against quadrants of colour behind when the absolute number become irrelevant – just a functional decoration.
pgk
13 November 2021 at 00:07 #571076 Michael GilliganParticipant@michaelgilligan61133Posted by drewt on 12/11/2021 20:15:49:Posted by Michael Gilligan on 12/11/2021 18:04:15:Posted by drewt on 12/11/2021 14:32:07:
Michael GilliganParticipant@michaelgilligan61133Posted by drewt on 12/11/2021 20:15:49:Posted by Michael Gilligan on 12/11/2021 18:04:15:Posted by drewt on 12/11/2021 14:32:07:[…]
IMAGE. The image mostly being used in this thread is of poor quality and suffers from being a composite (as some have noted), being low print resolution, and not accounting for parallax error. The original scans were high-resolution (0.05 mm) X-ray computed tomography (CT) imaging and performed in 2005.
[…]
.
One observation on that, if I may, Drew
Admittedly, I was working with an inferior image for my own efforts … but I did express some concern that your team was using XY co-ordinates based on 0.05mm resolution.
Frankly, I do not think that it is possible to reliably extrapolate the number of holes in the full circle when you are using rectangular co-ordinates at that resolution.
Crude as it was … I believe that my technique of directly estimating the angles [using an up-scaled, resampled, image] might have the potential to produce a better result.
MichaelG.
Michael,
I am very happy that people are questioning this work and methods. So, please do so.
Yes, we'd like higher resolution also. But, a couple of things are important about the question "is there enough resolution?" at least in my view. First, resolution helps more accurately define the edges, the specificity of the circle. Assuming the resolution is roughly the same around the circumference of a hole, the "errors" tend to average out. Not, of course, perfectly, but pretty reasonably below 0.05 mm, say somewhere between 0.025 and 0.035. Secondly, multiple measures of the same center points reduces this error by averaging the measures. I think this is noted in the paper, but we took multiple measures of the same hole (at different points in time to avoid our own bias) until we reached measurement saturation, that is, the X,Y center point became fixed within ≤ 0.05 standard deviation; we actually reached 0.037 mm. The value of statistics is it allows us to deal with these ambiguities by measuring errors and conveying a confidence and standard error value. While I agree higher resolution would be better, the resolution is very adequate for testing 365, but not adequate to confirm 354. This is evidenced by the fact we have a p-value for 354 of 0.005 and a p-value of 365 as 0.102 on the TOST procedure.
On the alternative measure of angles. We considered this early on and Chris, in fact, had done some work similar to what you have done. The problem is, to measure an angle you have to presume a center point. Since there is only a fraction of the circle available, and that is fractured, establishing a center is quite variable—so much so it would not reduce variability to a significant level. To also prevent others from suggesting we were cherry-picking the center point (which does not physically exist), our goal was to determine the center using only extant physical features. Once we'd concluded the center, we did go back and perform the same angle calculation you are doing and they line up surprisingly well at 354 days.
Finally, I think it may be important to define your term "better result." To me, that's a better standard error, higher confidence, lower variation caused by measurement error, etc. None of the authors really have a horse in the 365/360/354-day outcome, we just want the extant physical features to generate data we all can rely on to better understand the Mechanism.
Hope this helps. Again, feel free to disagree.

Drew
.
Thanks again, Drew … and my apologies for writing rather hastily there [I was due to leave the house very shortly, to listen to a talk by Jim Arnfield [not an opportunity to be missed].
My “better result” comment is based on the human factors side of performing the task … I believe that by resampling the image at 5x, I produced ‘softer’ images of the individual holes; in which it is easier to estimate the centre [and arguably therefore produce a “better” result than can be achieved with coarser pixellation].
Please forgive me if I confused your work with that of others … but I took the marking of Hole_1, as referenced in my post of 05/10/2021 22:50:01 , to be an exemplar of the problem … the centring looks hopelessly astray.
As for the notional centre of the ring … I simply used your value.
My own results indicated that 352 might be a good candidate [and I invited others to repeat my efforts and compare, but no-one stepped forward] … I did however convince myself that there is not sufficient detail to confidently estimate the count. My estimate is sufficiently close to yours that either could be correct … the difference is, I believe, lost in the noise.
If I can access the image that you used, then I may have another try … My first attempt was made using what I thought was the best available to me.
It’s a very interesting exercise !
MichaelG.
13 November 2021 at 00:08 #571077John McNamara
Participant@johnmcnamara74883Hi All
Using the second set of observations I made shown in green I calculated 355,83deg. This used the larger fragment with no visible cracking. I guess this larger fragment offers the best approximation accuracy available.
The method used was to visually place small circles over the “points” then apply an arc over the circles using eyeball best fit analysis.
Can we assume the points were holes? If they are holes I would be very interested to know if the “silt” mentioned previously by Drewt contained iron, particularly at the bottom of the holes? Maybe this would suggest pins protruding that might suggest a pin gear.
Getting back to the method. I would like to try it on the best available known image. If available online I would appreciate a link. I will repeat my test using this image.
I am somewhat confused by the apparent inaccuracy of some of the points, I firmly believe that a person capable of constructing this mechanism will have been capable of better hole placement.
Maybe we should ignore certain outliers from the calculations. Local corrosion might possibly have moved the apparent hole in the substrate.
Additionally, there is the possibility of larger (not visible) cracks deforming the substrate.
I look forward to a retest on a better image if found.
Edited By John McNamara on 13/11/2021 00:09:54
13 November 2021 at 02:50 #571081drewt
Participant@drewtMichael,
I agree with the better result and, for me, the practical outcome would be we could confidently test 354 or 360 days. Right now all we can say is what it's not (not 365) not what it is (at least between the popular calendar-day choices.
No problem on the image. A couple of things, we used "1" as the starting hole to follow tradition and not confuse others who, like me, get to know the holes by their number (a consequence os spending so much time with our little friends). Zero would make more sense. If you look at our composite image, and then our Figure 4, you'll see we ignore Section 0 (Hole 1, and inter-hole distance from 1 to 2). BTW, the Section numbers we define are based on measured breaks in the device. These are a new contribution to the understanding of the Mechanism.
On using our center, since we know there is already variation built into that center point (due to things you and others have mentioned—resolution, measurement error, etc.), using that as a starting place already picks up an error, This is why we applied a "first principles" approach and wanted all our data to based on primary, extant, physical features rather than some extrapolation.
Attached is our Figure 2, a composite that is planar to the channel and decent (but not full) resolution. For imaging, the next step up from this is the rendered CT files. 8.9 MB per image, hundreds of images just to cover the holes' depth.
13 November 2021 at 02:59 #571082drewt
Participant@drewtPosted by John McNamara on 13/11/2021 00:08:25:…
Can we assume the points were holes? If they are holes I would be very interested to know if the “silt” mentioned previously by Drewt contained iron, particularly at the bottom of the holes? Maybe this would suggest pins protruding that might suggest a pin gear.
Getting back to the method. I would like to try it on the best available known image. If available online I would appreciate a link. I will repeat my test using this image.
…
John,
It's for sure not iron and there are pretty good explanations of how/why the holes would have been used. Chris, for example, describes a very plausible use in the BHI article, part #2. In discussing the Mechanism with Andrew Ramsey, who took the CT scans, he felt there was even very little bronze left (much less if it was iron) as the metal has been chemically substituted over the centuries. There are a couple of papers about this process along with tests on bronze in seawater. This is not an area I know a lot about, but it's pretty clear the channel was designed to have the calendar ring ride in it and the holes were for alignment. Chris provides, in my view, an excellent explanation as a possibility.
I have attached, to the previous post, the best available single image. Feel free to use it but it is copyrighted material so citing the BHI article would be required if it was used to publish. Beyond this image, as noted in that post, the next step up in quality is a big one with hundreds of 8.9 MB images, each a 0.05 mm slice of the Mechanism.
Best,
Drew
13 November 2021 at 07:50 #571092Andre ROUSSEAU
Participant@andrerousseau66124Hi Neil, I knew you couldn't escape the alluring clutches of the A.M.! The 'ClickSpring' YT videos are superb but what you may not realise is that 'ClickSpring' is a wry play on his initials. But far more interesting is that in the course of his construction of his A M. replica he made a significant technical discovery that a whole lot of so-called experts had not previously twigged to. He co-authored a formal, peer-reviewed paper describing it which was published in one of the horological journals. It's freely accessible online.
Where I differ with one of his videos describing the archaic circle-division method he suggests the constructor used, is clearly ludicrous for some of the large hole-counts and undoubtedly the builder would have used the linear tape division method around the rim of a disc. Pretty obvious really and as other posters have already suggested.
Bear in mind that the builder was no wide-eyed 'newbie'; he clearly had had practice and with experience, a steady hand and much care surprisingly accurate results can be obtainable.
-
AuthorPosts
- Please log in to reply to this topic. Registering is free and easy using the links on the menu at the top of this page.
Latest Replies
Home › Forums › General Questions › Topics
-
- Topic
- Voices
- Posts
- Last Post
-
-
Injectors
Started by:
pansy123 in: General Questions
- 6
- 7
-
3 July 2025 at 07:05
Dave Wootton
-
Twin Engineering’s heavy mill/drill quill removal
Started by:
Martin of Wick in: Manual machine tools
- 8
- 18
-
3 July 2025 at 06:20
Diogenes
-
Pattern Makers Vice
Started by:
 Vic
in: The Tea Room
Vic
in: The Tea Room
- 7
- 9
-
2 July 2025 at 21:51
 KEITH BEAUMONT
KEITH BEAUMONT
-
J&S grinder – belt which way ?
Started by:
gerry madden in: Manual machine tools
- 7
- 9
-
2 July 2025 at 21:44
not done it yet
-
Meddings MF4 Manual
Started by:
Richard Kirkman 1 in: Help and Assistance! (Offered or Wanted)
- 11
- 23
-
2 July 2025 at 21:38
Richard Kirkman 1
-
Haining vertical dairy engine boiler.
Started by:
apprentice in: Beginners questions
- 3
- 7
-
2 July 2025 at 20:52
 JasonB
JasonB
-
Speed camera
1
2
Started by:
 David George 1
in: The Tea Room
David George 1
in: The Tea Room
- 20
- 39
-
2 July 2025 at 20:01
Plasma
-
Motor won’t start
Started by:
Rowan Sylvester-Bradley in: Beginners questions
- 9
- 9
-
2 July 2025 at 17:30
larry phelan 1
-
IME Watchmakers lathe
Started by:
Greensands in: Manual machine tools
- 11
- 16
-
1 July 2025 at 21:41
Dave S
-
Request for a Slot to be Milled in a Shaft
Started by:
James Alford in: Help and Assistance! (Offered or Wanted)
- 9
- 18
-
1 July 2025 at 21:03
bernard towers
-
Bearing boxes for ball race
Started by:
Paul McDonough in: Beginners questions
- 9
- 17
-
1 July 2025 at 21:02
Paul McDonough
-
The Stevenson Trophy – Entries Invited
Started by:
 Neil Wyatt
in: Website Announcements
Neil Wyatt
in: Website Announcements
- 1
- 2
-
1 July 2025 at 18:44
 Neil Wyatt
Neil Wyatt
-
The Bradford Cup – Nominations Wanted
Started by:
 Neil Wyatt
in: Website Announcements
Neil Wyatt
in: Website Announcements
- 1
- 2
-
1 July 2025 at 18:41
 Neil Wyatt
Neil Wyatt
-
FreeCAD v1.0 tutorials
1
2
3
Started by:
 Michael Gilligan
in: CAD – Technical drawing & design
Michael Gilligan
in: CAD – Technical drawing & design
- 12
- 54
-
1 July 2025 at 18:31
Speedy Builder5
-
All things Beaver Mill
1
2
…
8
9
Started by:
Robert James 3 in: Manual machine tools
- 43
- 208
-
1 July 2025 at 18:22
Charles Lamont
-
Dial test indicator vs Dial indicator
Started by:
martian in: Workshop Tools and Tooling
- 17
- 24
-
1 July 2025 at 16:59
Clive Foster
-
Help for DIY lathe build.
1
2
Started by:
moogie in: Help and Assistance! (Offered or Wanted)
- 16
- 32
-
1 July 2025 at 15:21
David Senior
-
Firth Valve Gear
Started by:
Andy Stopford in: Traction engines
- 9
- 18
-
1 July 2025 at 12:59
Nigel Graham 2
-
M type top slide conversion??
Started by:
jimmyjaffa in: Beginners questions
- 7
- 11
-
1 July 2025 at 11:35
 David George 1
David George 1
-
Offen screw type telescopic gauge.
Started by:
Graeme Seed in: Workshop Tools and Tooling
- 4
- 9
-
1 July 2025 at 10:41
Graeme Seed
-
2 Machine lights
Started by:
modeng2000 in: Workshop Tools and Tooling
- 2
- 6
-
1 July 2025 at 08:57
Dalboy
-
New member looking for help
Started by:
 manfromthemist
in: Introduce Yourself – New members start here!
manfromthemist
in: Introduce Yourself – New members start here!
- 11
- 24
-
1 July 2025 at 08:19
Juddy
-
Wiring up a single phase AC motor with 4 wires
Started by:
ell81 in: Beginners questions
- 6
- 8
-
30 June 2025 at 19:49
Howard Lewis
-
New (old!) member
Started by:
iansoady in: Introduce Yourself – New members start here!
- 3
- 3
-
30 June 2025 at 19:30
Howard Lewis
-
Boiler Design – issue 4765
1
2
…
7
8
Started by:
Charles Lamont in: Model Engineer & Workshop
- 26
- 178
-
30 June 2025 at 12:58
Paul Kemp
-
Injectors
-




 . For clarity, the authors look at this as one article but BHI, wisely, split it into two, one about the finding, and the second about the implications. I will refer to it all as one article.
. For clarity, the authors look at this as one article but BHI, wisely, split it into two, one about the finding, and the second about the implications. I will refer to it all as one article.



