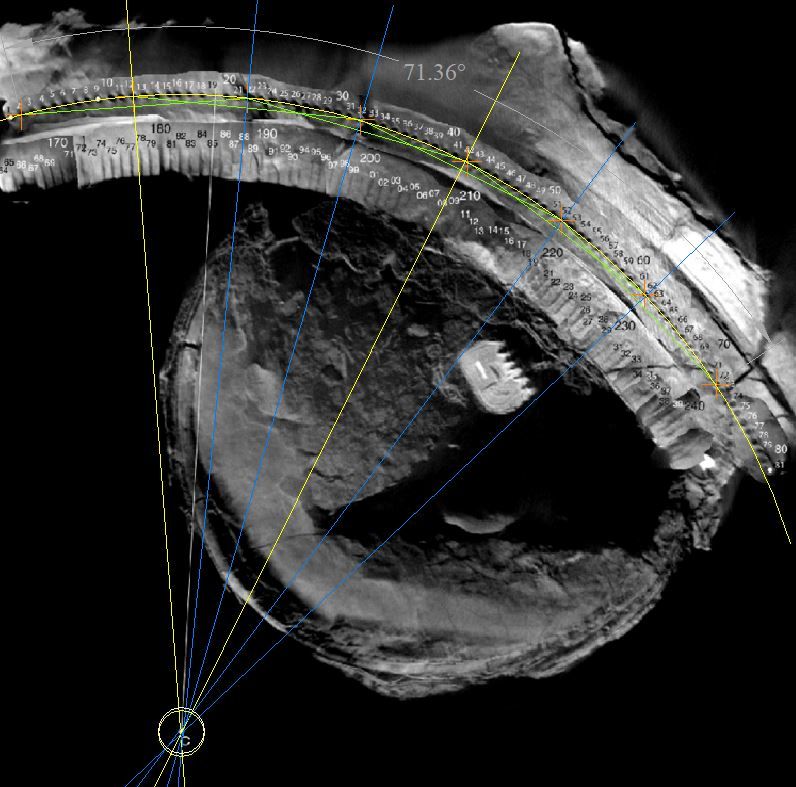
Antikythera Mechanism
Antikythera Mechanism
- This topic has 211 replies, 40 voices, and was last updated 17 November 2024 at 01:44 by
david bennett 8.
- Please log in to reply to this topic. Registering is free and easy using the links on the menu at the top of this page.
Latest Replies
Viewing 25 topics - 1 through 25 (of 25 total)
-
- Topic
- Voices
- Last Post
Viewing 25 topics - 1 through 25 (of 25 total)
Latest Issue
Newsletter Sign-up
Latest Replies
- Easiest/cheapest source of R8 socket
- Please direct me to where I can find an engineer to do some bespoke work
- How many spokes do I really need?
- What Did You Do Today 2025
- Model Engine running just off a naked flame
- Herbert B drill information?
- Which lubricator do I need
- Even the Dealer Didn’t Know!
- Backplate studs
- William Hazeldine … Proving Machine