Hi John.
MOD does what it's supposed to. And for what we are trying to do, it has more merit than most.
The trouble is that I was using it in a way that just wasn't correct for what I had wanted to achieve.
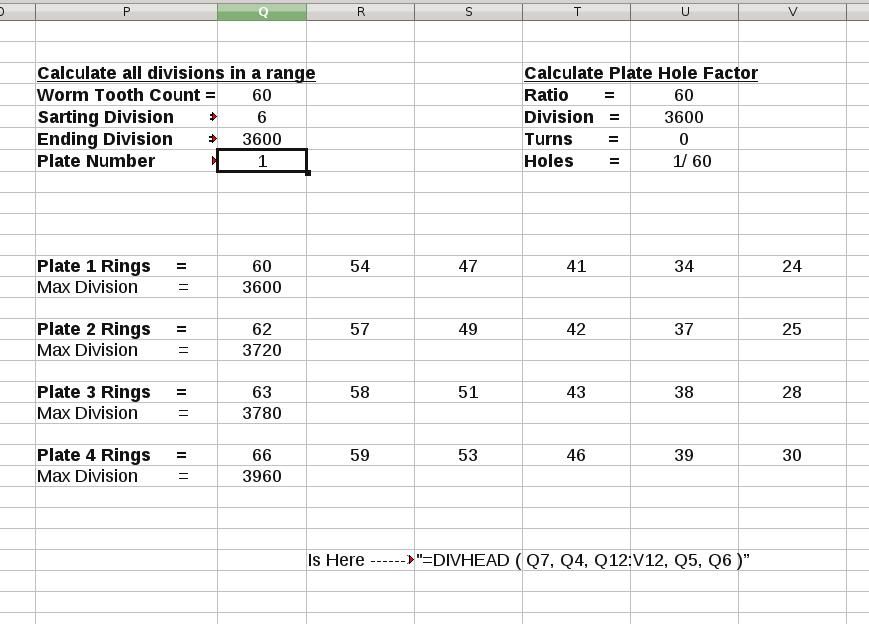
Because of that, the spreadsheet wasn't reporting all of the possibilities that it should have.
I know you have mentioned the business of floating point arithmetic quite a number of times. I don't know how to say this tactfully, but I just don't buy into it. I don't think there is anything wrong with using fractions, but I am also completely satisfied that decimals are just fine too. The floating point unit in any machine capable of running windows, can do this sum with enough precision that you could index individual atoms if your dividing head was up to it.
If you look you will see that I have explicitly set zero. I figure anything less than 1×10−12 to be "zero". If there is an error less than this then it isn't worth worrying about. Bear in mind that an atomic nucleus is considered to be 1.75×10−15 of a metre. This is not an uncommon issue when using floating point numbers.
The best example is comparison. In software, although you can compare two floating point numbers to see if they are equal, there is almost no point in doing so. When you think about it, that is quite reasonable. With so much precision there is almost no chance that two different quantities will be the same.
Generally the computer is less good at handling values with reoccuring decimals. This is because it only "appears" to have limitless precision. It is true to say that fractions can help humans deal with these scenarios. If you know you want the computer to do the grunt work, then I think it's decimals, all the way.
It's not actually decimals which are the problem. It's the computer. If you were to write down the whole string of a decimal, then it would be just as good as a fraction. The computer does not do this because it's designers knew better. As it happens the floating point unit is more or less a fraction machine. The mantissa and exponent are an expression in base 2 scientific notation. Nevertheless they work together almost the same way as fractional values.
As an example, floating point numbers are regularly "normalised" by the computer. This process is the same as reduction of an improper fraction. One of the main departures is that the computer does not attempt to distinguish units. It does not try to say 1 7/8 it just says 15/8. During calculation it might arrive at the quantity 30/16 which would be "normalised" to 15/8.
You have to bear in mind that I have simplified this. the sums it performs are actually in base 2. I did that example in base 10 just to make it obvious.
You might be able to choose the right fraction to deal with a reoccuring number, but the computer has no way to do that. The real observation is that I am sure that the computer is prepared to maintain more digits in it's floating point "fraction" than any human ever would be bothered to. In my opinion on precision, with floating point numbers pitted against inspired human fractional choices, you win some, you lose some. The main thing is that the computer does what it does FAST.
Don't forget that I'm not insisting that you use my spreadsheet. I fixed it because a fault was raised and I didn't want to lead anyone astray.
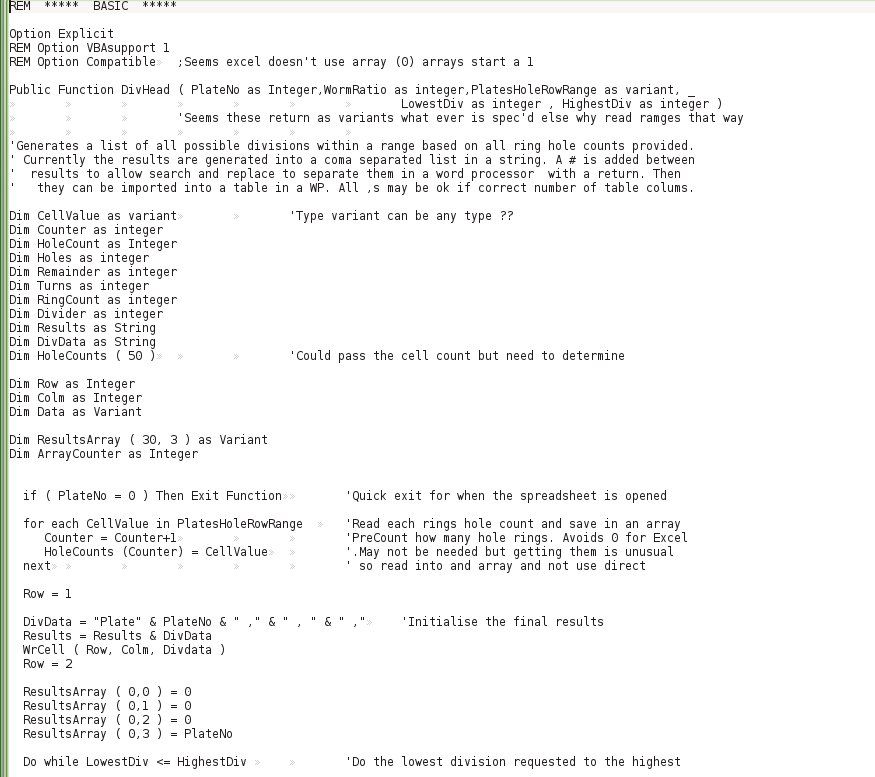
I think using the variable precision is an extremely useful tool. To use it well one must understand what it can and cannot give.
Ajohnw.


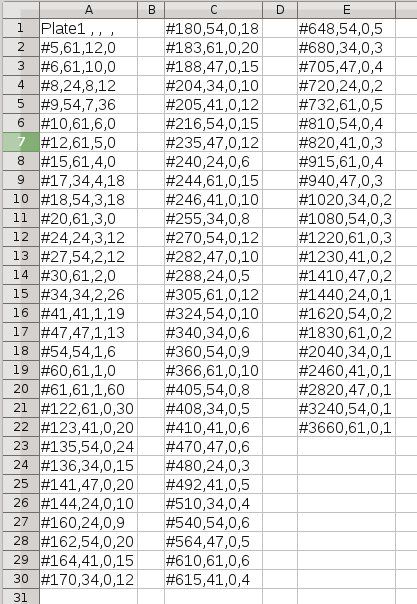
 No tables available for my plates Tony.
No tables available for my plates Tony.