Depending on the frequency of the square wave, the high pass filter here

RC, RL, LC Passive Filter Calculator | DigiKey Electronics

should help you calculate.

You might want to put a second smaller capacitor across the  speaker as a low pass filter to take out the high harmonics in the square wave.

Duncan

We need some more information in order to answer your question properly.

You say you are driving the speaker with a square wave off 24 volts. Do you mean the square wave has an amplitude of 24volts, and is it 0-24 volts, or +/- 12 volts?

What is the impedance and power capability of the driving source, and what is the frequency of the square wave?

If the source is low impedance and the amplitude really is 24 volts peak to peak it will likely destroy your 8 ohm speaker rated at 1 watt, or itself be destroyed. If the source is high impedance it may be incapable of driving a low impedance speaker.

More info needed.

On 21 December 2023 at 20:40 Neil Wyatt Said:

A 24V square wave will put about 18watts into an 8 ohm speaker. …

Neil

Is it me?  I reckon 72W from W=V*V/R

Maybe Duncan has a 72W amplifier, but I took him to mean he had a 24V rail, with a resistor being grounded by a transistor driven by an arduino.

For a 1W 8 ohm speaker, I reckon a 2W 470ohm dropper resistor , capacitor what I said above.

Dave

Don’t forget your Zobel Network 🙂 ok not necessary for just an alarm.

Now before I double checked I was sure these used to be called Ziegler Networks, is that just old age or anyone with me?

On 21 December 2023 at 23:13 duncan webster 1 Said:

If the speaker was in series with a transistor across the 24v Dave’s sum falls down as its only conducting half time, so 36W

…

Time is a vital factor in Duncan’s question, so all our guesstimates are a bit suspect.   Also, we’ve all made assumptions, with Neil assuming a 24Vrms amplifier, whereas I assumed a 24Vdc rail.   Both wrong, Duncan now says it’s a 5V rail!

Anyway, consider what happens in my circuit above.

• the rail holds steady at 24V (unless the power supply is rubbish!)
• when the transistor switch is OFF, the capacitor charges via the 470ohm resistor and the speaker.  Doesn’t charge instantly, because the 470ohm resistor inhibits current flow, as does the speaker, a bit.   The speaker’s cone moves OUT in time with the current flowing in the capacitor as it charges up.
• when the transistor is switched ON, the capacitor discharges through the 8ohm speaker.  Current flow in the speaker is reversed, and the cone pulls IN.   The 470ohm resistor does nothing beyond wasting a few DC watts.  Instead the time taken to discharge the capacitor is proportional to its value and the 8ohm inductance of the speaker.  My earlier post calculated the capacitor needed to resonate with the speaker, more explanation below.  For this I took time into account, hence 2πf in the formula; C varies with frequency.
• The amount of power that can be delivered to the 1W rated speaker is limited by the 470 ohm resistor.  The circuit doesn’t apply the full power available from the 24V rail to the speaker.

There’s a Resistor/Capacitor time constant calculator here.  At 24V, 470ohm and 47µF it says:

Note the graph shows that the charge current flowing in the speaker isn’t a square wave. The sharp rise is converted into a rounded curve by the RC time constant.   Not a sine wave, but far from square.

Different maths applies when the transistor switches ON and shorts the capacitor to ground.     This speaker coil is an inductor, not a resistor, and inductors also have a time constant.   Inductors and capacitors both store energy, but they do so in the opposite sense.  Thus, when a capacitor discharges into an inductor, it charges the inductor.  Then the current flow reverses and the inductor discharges into the capacitor.  The LC time constant is resonant at some frequency, so LC circuits oscillate at a particular frequency, and the output is a sine wave.

My circuit is akin to banging a drum.  The transistor switching OFF sends a rounded pulse of energy into the speaker cone.  Shortly after, switching ON causes the LC combination to oscillate.

If the speaker was a perfect inductance, the LC combination would oscillate for many cycles, and the output would be a sine wave.  Speakers are far from being a perfect inductance though. Some energy is lost as heat due to wiring resistance, and a massive amount due to stirring air with the cone.  The speaker is more motor than inductive load, mechanically converting electrical energy into sound.  Accelerating the cone and pumping air also take time, making the exact waveform hard to predict accurately.  Something like this though:

Much closer to a sine wave than square.  In terms of power consumption the waveform is roughly 50% duty cycle.  Duncan’s idea of using Pulse Width Modulation is interesting.  PWM produces a rectangular wave with a duty cycle anywhere between  05 and 100%, his choice.   In effect, PWM allows the drum to be beaten more or less heavily, altering volume and the wave shape.

Maths and theory applied competently get circuit values in the right ball-park.   In this case, I’d experiment for best results.  For example, the speaker will be most efficient when the electrical resonance is tuned to its mechanical resonance.  However, this could be too much for the construction, as when opera singers shatter wine glasses!  A cheap speaker rated for 1W with a normal audio spectrum, might not be able to sustain that promise at resonance.  (More expensive speakers are designed to avoid resonances within their operating range because resonances disturb music lovers.  Done by reducing speaker efficiency, which is why I suggested a ceramic disc.  They go for maximum efficiency at a particular tone, producing a nasty waveform that’s very loud!

Beware: I often get maths wrong, and haven’t tested my conclusions by wiring one up!

Dave

On 21 December 2023 at 23:13 duncan webster 1 Said:

If the speaker was in series with a transistor across the 24v Dave’s sum falls down as its only conducting half time, so 36W

I think Neil’s sum is based on a sine wave. Interweb says square wave delivers twice sine wave for same peak to peak. This website explains it without a capacitor https://electronics.stackexchange.com/questions/299571/how-to-calculate-the-average-power-for-a-square-wave-dc-signal/299578#299578

However I must have been having brain fade when I asked the question, I have 5v derived from a 7805 to drive the Arduino, so I can use that to drive the speaker, with a 5 ohm series resistor. It’s also dawned on me that I could use the pwm output and drive less than half time, something to experiment with over Xmas

It depends.

I assumed a 24V square wave relative, as in 0v-24v, not a sine wave.

But my calculation assumed a large capacitor was used to decouple the square wave, so it would be alternating between +/- 12V across the speaker, so the average RMS voltage would be SQRT((12×12 + -12x-12)/2) = 12.

For a sine wave a 24V P-P signal would give 0.707 times that value = ~9V.

If the square wave is connected directly across the speaker without a decoupling capacitor, it alternates between 0v and 24V so the RMS value is SQRT(24^2/2) = ~17V

On 22 December 2023 at 13:20 Neil Wyatt Said:

Maths and theory applied competently get circuit values in the right ball-park.   In this case, I’d experiment for best results.  For example, the speaker will be most efficient when the electrical resonance is tuned to its mechanical resonance.  However, this could be too much for the construction, as when opera singers shatter wine glasses!  A cheap speaker rated for 1W with a normal audio spectrum, might not be able to sustain that promise at resonance.  (More expensive speakers are designed to avoid resonances within their operating range because resonances disturb music lovers.  Done by reducing speaker efficiency, which is why I suggested a ceramic disc.  They go for maximum efficiency at a particular tone, producing a nasty waveform that’s very loud!

Beware: I often get maths wrong, and haven’t tested my conclusions by wiring one up!

Dave

I’ve been majorly misinterpreted!

I suggest Dave you look at en.wikipedia.org/wiki/Thiele/Small_parameters and download WinISD.

For most speakers, the resonant frequency is effectively their low-frequency cut-off, below which the speaker becomes less efficient. You can’t avoid the resonance of the driver, it’s an inherent property of the driver. What you do is tune the enclosure (either by choosing a specific volume or making it into a tuned cavity by using one or more ports) to flatten out the resonant peak into an extended bass response. …

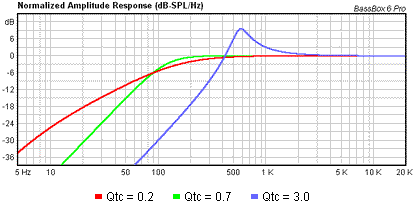
Below in the blue example the resonance at 600Hz could cause problems (Qtc is the inverse of the damping ratio i.e. a measure of resonance).

The green line is an ‘ideal’ response for a flat response speaker.

The red line is over-extended so you don’t get any useful extension compared to the green line.

…

Not misinterpreted, rather Neil and I are at cross-purposes.

I was tightly focussed on the electronic aspect of Duncan’s question : how to drive a 1W 8Ω speaker with a square wave.  Nothing HiFi about Duncan’s requirement – his application is an alarm, where loud and piercing are the bees knees, not bass response.

Neil’s comments address a different aspect of loudspeaker design – how best to enclose the mechanical speaker.  The box a speaker is mounted in is important too, especially when playing music.  But this is acoustics rather than electronics.  Acoustic engineering also deals with the resonance and distortion of waveforms, but they’re sound waves moving in air.   And it’s complicated – the speaker and its enclosure have to be optimised, and then – ideally – the room matched to the speaker.  Thought the Sydney Opera House has a striking exterior, I’m more impressed by the audio performance of its interior.

Anyone else remember the good old days at Paddington, where announcements sounded like: ‘The tra, tra, ain, now ow ow, st, st, anding a at Pla, pla t form, rm, two oo oo is the nu nu ine ten for Ca ca ard if if’.  This was the best a 1930 PA system and horn speakers could do in a big echoing building without spending a fortune!

HiFi takes engineering design into complicated territory.  In Neil’s bass guitar, the pick-up will have been designed to produce a flat response over the range of tones produced by the strings, and although it will also do a good job with overtones and harmonics, higher pitched guitars are probably fitted with pick ups that suit their frequency range.   These pick-ups need to be accurate rather than efficient, because low signals are easily amplified electronically.

The signal is normally fed into a pre-amplifier, designed with a flat response to increase the signal level without distorting it.   The output could be fed directly into a power amplifier, but more likely there will be a processing stage.  The processing could be as simple as a Tone control, or a basic graphic equaliser, or an advanced graphic equaliser plus other gizmos.   The purpose, in so far as possible, is to compensate electronically for shortcomings in the pick-up, amplifiers, and loud speaker system.

In my youth, audio systems were entirely analogue.  Worked well if a lot of money was spent on them, but with many limitations, and they were noisy and tended to sound a little mushy or other wise tainted compared with live music.  Filtering is particularly difficult to do well with analogue components, for example a sharply tuned high-Q inductor/capacitor combination rings like a bell because the components store energy.  The filter has to be backed off to avoid ringing, not good.

Digital processing is much better at cleaning up and manipulating signals than analogue.  The signal is converted into a stream of numbers that can manipulated mathematically.   Implementing a digital filter that doesn’t ring no matter how sharply tuned is trivial.  A bit code like:

getInput:
read sample
if sample < 999.9 or sample > 1000.1 then goto getInput

And much, much more can be done.  See Cher Effect which was a novel use of Autotune – a device that corrects off key singers on the fly, so what reaches the speaker is correct.

Fascinating stuff and worthy of long discussion, but a long way from Duncan’s requirement, which is how to make an Arduino make a nasty noise as an alarm!

Dave