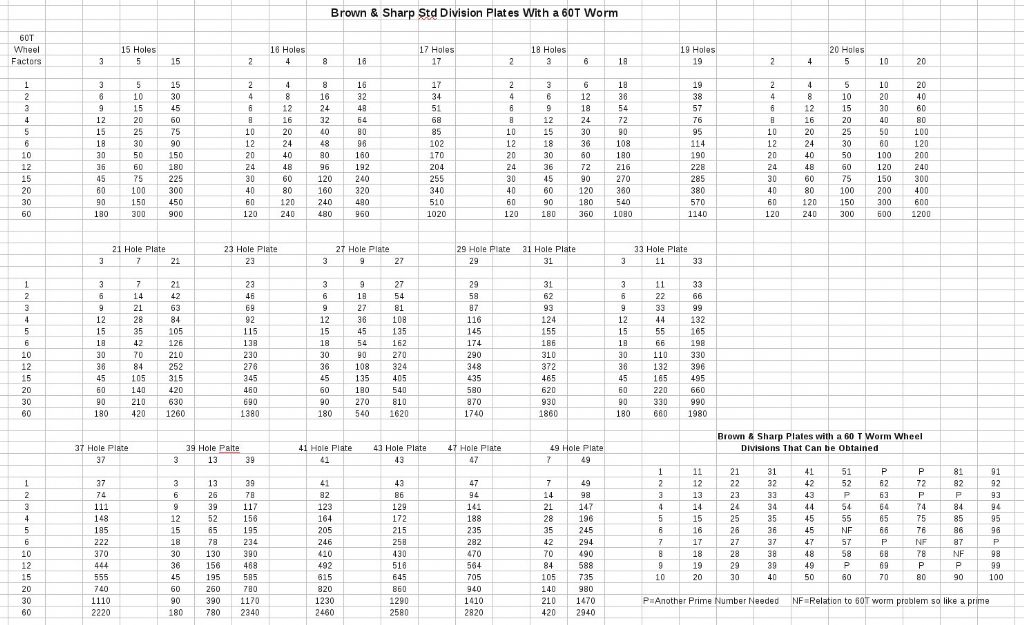
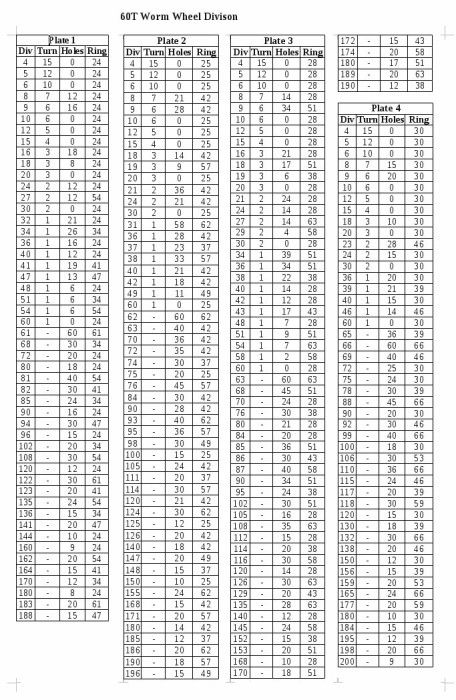
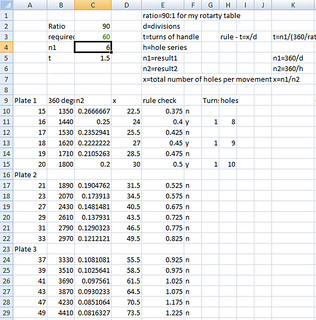
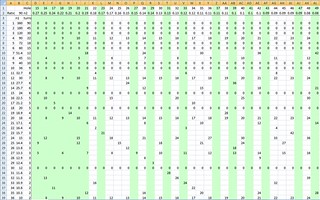
I have a spreadsheet I wrote (still looking for somewhere I can post it so others can have access if they are interested).
It has 2 tabs, one where you list out the holes in your plates, set the worm ratio, enter the required division and it will show you which plates are capable of solving it.

The other tab is a huge table that has divisions down the left and plate holes along the top, this one shows every solveable division within that range, again, you just enter your worm ratio.
It shows both turns and holes to move in order to solve a given division, there is also a column at the end that shows, based on the plate holes provided, whether or not a particular division is possible.
The solve is possible if n1 ( 360/divisions ) divided by n2 ( 360/(holes*worm ratio) ) is an integer, this value is the number of holes to use in addition to the number of turns ( integer(n1/(360/worm ratio)) ).

Additional plate holes can easily be added (just an additional column)
The spreadsheet currently solves for every division from 1 to 360, additional divisions simply require more rows, or just a custom row that shows the division required.
Another thing to bear in mind is that just because you can't solve a particular division with the plates you have, does not necessarily mean that you can't make a plate that can solve it quite easily.
Using the above example of 125 divisions, my worm ration of 90 and my available plate hole sets of 15, 16, 17, 18, 19, 20, 21, 23, 27, 29, 31, 33, 37, 39, 41, 43, 47, 49, it would appear that I do not have a plate that can solve for 125, however I can easily make a plate, using the plates I already have.
125 divisions can be solved with 25 (0 turns and 18 holes) or 50 (0 turns and 36 holes).
25 divisions can be solved with 15 (3 turns and 9 holes) or 20 (3 turns and 12 holes), both of which are in my standard set.
50 divisions could also be solved with 15 (1 turn and 12 holes) or 20 (1 turn and 16 holes).
I intend to make a 4th plate for my dividing set that has 25, 63, 67, 68 and 71 holes, as these add additional useful numbers.
The main area where the intermediate aproach would break down is for prime numbers such as 67, 71 and 127, this is one of the reasons why I have made my Division Controller, (I need to make a 127 tooth metric translation gear for my lathe), which once up and running will largely render the division plates redundant.
Edited By Timothy Moores on 18/05/2016 09:41:30
Ajohnw.


 Anyway I wonder if anyone has come across an application that generates a table of all a set can do over some specified range of divisions.
Anyway I wonder if anyone has come across an application that generates a table of all a set can do over some specified range of divisions.