Rather than clutter up the 'What did you do today?' thread I've started this thread to discuss the design and machining of a worm and worm gear for the steering gear on a 4" scale traction engine.

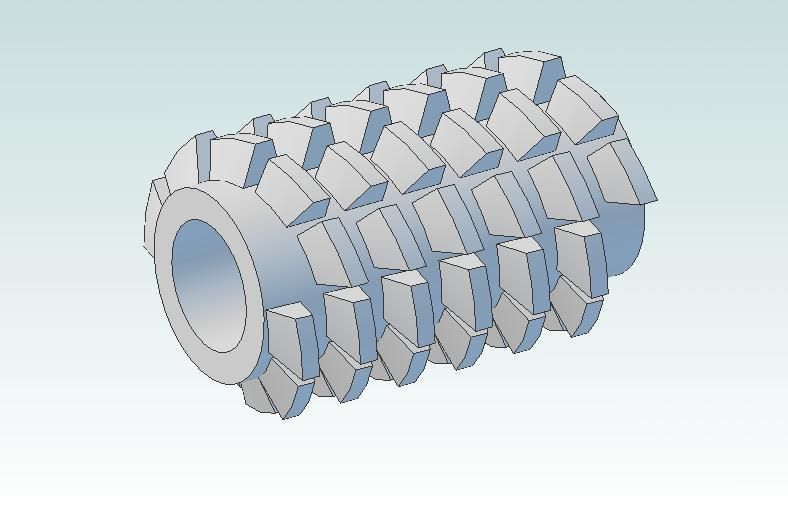
The drawings call for a 2 start worm with a pitch of 1/2" and an OD of 1.48", plus a quoted lead angle. There is no detail about the thread form, depth or anything else, and the lead angle quoted is wrong. The thread form is diagrammatically shown as Acme, which seems reasonable. My lathe will cut 2tpi, but not the 1tpi as required for the two starts. That left me with two choices for cutting the worm. One, use the vertical mill and a series of ever smaller cutters while driving the dividing head from the table to get the helix. Two, use the vertical head on the horizontal mill with an involute style cutter to cut the thread in one pass, again driving the dividing head from the table. I don't have the requisite 'involute' cutter, so step by step it is. In which case I might as well do it on the CNC mill, as it's less effort. My CAM program can only do 4th axis toolpaths parallel to the rotary axis, or round and round it. Neither is satisfactory; the ideal would be to follow the helix of the worm. So I hand wrote my own G-code, which turned out to be quite simple, just a series of G01 moves with arguments in X and A. At this juncture it was pointed out that a 2-start worm is wrong, as the front wheels will back drive the worm gear assembly. So I re-designed the worm as a single start. I could have cut this on the lathe, but since I was so advanced with the G-code I decided to stick with the CNC mill. I won't go into the details of the thread form, but I did change the included angle of the Acme form to 30°, rather than the more common 29°, as I could buy a 30° tapered endmill. The basic code and methodology seems to work well, the next task is to cut the worms in steel, rather than plastic like this:

I'll also get the hand correct, the worm is supposed to be RH, but the plastic demo is LH.

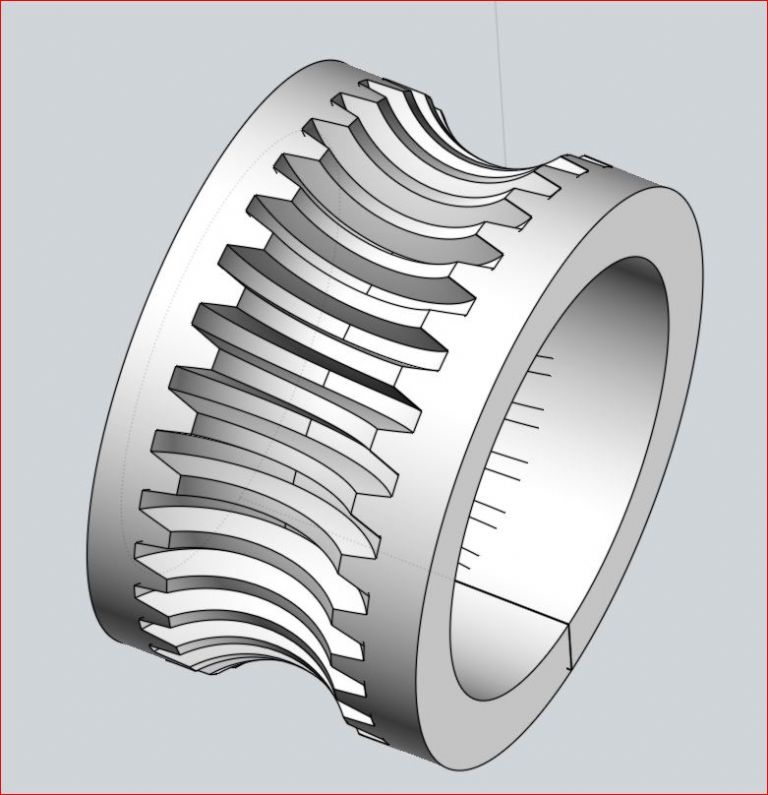
For the worm wheel the drawings show what is essentially a helical gear. Since the pitch of the worm is rational the DP of the mating worm wheel is irrational, so involute cutters will not be available. Furthermore I wanted a single enveloping worm wheel, not a helical gear. The obvious way to make this is by free hobbing, ie, the hob drives the worm gear as it is cut. I've spent a lot of time looking at hob design and drawing various styles of hob, like this:

However, I've decided that it is just too involved to make a hob with the proper form relief. I also looked at machining the worm wheel direct on the CNC mill. However, the tooth form required is very complex, and I miserably failed to draw even a rough approximation. So back to free hobbing it is. For the hob I am going to essentially machine a worm in silver steel, which can be gashed to provide some measure of relief, and then hardened and tempered. I intend to add extensions to the hob so that one end will fit into a Clarkson Autolock chuck and the other end can be supported by a centre.

As I make progress I'll update this thread.

Regards,

Andrew

Neil: My worm wheel will be 22 teeth with a DP of 6.283, so quite coarse teeth. Rather than relieve the teeth properly I intend to gash them such that the remaining teeth look like triangles. Thus the relief is obtained by removing most of the teeth. The hob only has to cut two gears, so it's unlikely it'll ever need to be sharpened.

JohnS: If I don't write code what am I going to run? I've written almost exactly what you posted, except that I use metric, so:

G21

blah blah blah tool change/spindle speed/coolant/rapid to start

G01 X76.2 A2160.0 F320.0 (3" and 6 turns)

Martin: How the xxxx did you do that? Extrude an involute tooth form at the lead angle around the PCD of the worm? I tried that and the result looked nice, but assembled with the worm the tooth shape was clearly wrong and didn't mesh properly. That's when I gave up trying to model the worm wheel teeth.

Here are two worms I've made in steel this evening, RH this time:

I'm not at all happy with them. It's all down to feedrates. I used three cutters; 6mm carbide at 4000rpm and feedrate of 420mm/min, 3mm carbide at 5000rpm and feedrate of 320mm/min and a HSS taper end mill at 1500rpm and 120mm/min. I thought that the rotary table didn't seem to be slowing down much on the slower feedrates. In fact it wasn't, I think it was flat out all the time. I'm amazed I haven't badgered at least one of the cutters.

Clearly I haven't got to grips with linear/rotary combined feedrates. I understand that if a linear motion and rotary motion are combined in G01 then the feedrate is taken as an 'unwrapped' linear rate, according to a rotation diameter correction factor. Here is where it all gets murky. Both the Mach3 and my mill manual talk about a rotation axis diameter correction, but on the screen it is shown as a radius correction. And does the computation take into account the number of turns the rotary axis makes? I set 16, thinking 16mm radius, but who knows how it is interpreted.

Needless to say neither manual actually gives any examples, or talks about units. I wonder if Mach3 only understands imperial for the correction factor? Certainly when setting the tool table the differential heights are shown in millimetres when taking measurements, but they're stored in the tool table in inches irrespective of G20 or G21.

I'm going to have to do some experiments by typing code into the MDI and timing the rotation of the rotary table.

Regards,

Andrew

JohnS: I'm using a Tormach CNC mill, which uses their own customised version of Mach3, so my screens are different to yours. However, you are correct, there are two places to enter the correction; on the main control screen, and on the settings page. Confusingly on the settings page it's listed as a correction diameter, on the main page as a radius.

I've done a few tests this morning to try and understand the feedrates. For G01 commands with an argument only for A and F it all works perfectly. The machine interprets the F in degrees/sec, and the movement of the table is spot on, according to the secondhand on my watch. However, when we introduce an argument for X as well, where the interpretation of F is supposed to be mm/min it all goes to pot. With the correction diameter set at 31.8mm, so that the circumference is about 100mm, the following code:

G01 X0.1 A360.0 F100.0

takes 3 minutes and 35 seconds. It ought to take 1 minute according to my logic. If I reduce the correction diameter to 15.9mm, half the diameter so for the same feedrate the table ought to turn twice as fast the code takes 3 minutes.

I tried everything in inches as well, and that didn't work either. If I use a correction diameter of 31.8mm and a feedrate of 358 then the rotary table does one turn in a minute.

The whole thing makes no sense at all to me; for a given feedrate the rotation speed is not directly proportional to the correction diameter, which it should be.

Regards,

Andrew

Martin: Thanks for the link. My rotary table has no problem with speed, it's getting a consistent feedrate when milling in both X and A that seems to be the issue.

However, after some more searching and fiddling I think I have the solutuion. First, there is an error in the Tormach version of Mach3, in that the correction diameter/radius is inconsistently labelled on the screens. Apparently the correction diameter is a red herring, it's actually the distance from Z=0 to the rotation axis. For my worm Z=0 is the rotation axis, but if you set zero you disable the correction function. So I set it at 0.0001, which enables it. Then, with Z=15.9mm, ie, a diameter of 31.8mm and a circumference of 100mm I did the following:

G01 X0.1 A360 F100

This actually took a shade over 30 seconds, instead of 60 seconds, but at least it's consistent. If you double the rotation degrees, or halve the feedrate, or double the Z value, then the time exactly doubles, as it should.

So it seems that Mach3 does the correction from the actual Z value of the cutter. But you have to set the correction diameter to a non-zero value to enable it, and for some reason the actual feedrate is twice that demanded. Presumably this is due to a foul up regarding radius versus diameter. At least the numbers and feedrate are now consistent, and scale as they should.

The next thing is to re-run my worm G-code and time the rotations to see that the feedrates are actually changing as I expect.

Regards,

Andrew

The plot thickens; in order to test my understanding of the feedrates I ran some more tests last night. As before I used the following code, all distances in millimetres:

G01 X1.0 A360.0 F50.0

With the radius correction set to 0.0001 and Z=15.9, the code took 1:03 minutes, pretty close to the desired 100mm/min feedrate. So far so good. It is always interesting to explore the limits, so next I tried the same code with Z=0.1, ie, not a lot! The code took 18 seconds to run. In essence the rotary table is running as fast as it can in an attempt to achieve the required feedrate. Again, pretty much as expected. Then I tried the code with Z=159, the code took 3:57 minutes, not what was expected, it should take about 10 minutes. What's going on? What else did I change? Due to the way my tool table is set up I had to change tools in Mach3 to get Z=159 without hitting the limit switches. Previous tests had been done with tool 0, ie, my master tool. For this test I selected tool 1. So it looks like the linear/rotary feedrate correction doesn't follow the changes in Z due to different tool lengths? If that's the case, then it's about as much use as a chocolate teapot.

After that debacle I did one more test, with tool 0 selected. This time the code was:

G01 X200.0 A360.0 F50.0

In other words quite a slow helix. The code took 4:20 minutes, which is about double what I would have expected.

Regards,

Andrew

The final worms are made! Like a lot of operations, once everything is sorted out the actual machining is a bit of an anti-climax. However, it is strangely mesmeric to watch the rotary table turn and a helix magically appear in the blank. Here are the tools used; from left to right, the master tool used to set zero and relative tool lengths, a 6mm cutter for initial roughing, a 3mm cutter for deeper roughing and a 30° included taper end mill for finishing:

The general set up:

And the final worms:

Why three worms? Because I'm making two engines, but I made three blanks just in case of a boo-boo in the machining.

Regards,

Andrew

More progress; here's the embryo hob, in silver steel:

Next job is to gash it and then harden it. Before I do that though I need to decide how many gashes (current thinking is 7) and make sure I have the direction correct. The hob will fit into a SKF Fastloc (Clarkson Autolock lookalike), so I need to make sure that the cutting forces tend to tighten the cutter into the chuck.

Regards,

Andrew

Muzzer: Yes, my camera does have video mode, although whether I have time to video the first attempt is a different matter. Forget analogue, machining is digital! There are no half measures; it's going to be a case of set everything up the way I think it should be, and then drop the clutch and stand back. It'll either work or disintegrate in short order. The horizontal mill won't care either way. A 5hp motor geared down to 50 rpm will just spit out the bits if I get it wrong.

Stub: I understand the idea of having the hob at full depth and moving it across the blank, but I assume that will generate what is essentially a helical gear? I am aiming for a single enveloping worm wheel rather than a helical gear. Machining a helical gear is pretty straightforward, so I thought I'd have a go at a 'proper' worm wheel instead. The plan is to gash the wheel beforehand. The books say to use an involute cutter of the appropriate DP and number of teeth and of similar diameter to the worm. Since the linear pitch of the worm is rational the DP of the worm wheel is irrational, in fact it is 6.283 etc. I happen to have a 6DP involute cutter for 21-25 teeth which is pretty close. However it is quite a bit bigger diameter than the worm, so I won't be able to get full depth. I'm not sure what effect this will have. I could try and make a special involute cutter as well, but I'm tempted to just give it a go and see what happens.

Regards,

Andrew